Each question contains statements given in two columns which have to be matched. Statements a,b,c,d in column I have to be matched with statements p,q,r,s in column II. If the correct match are a-p, a-s, b-r, c-p, c-q, and d-s, then the correctly bubbled 4 x 4 matrix should be as follows: fig Column I, Column II If L=(lim)x→−1(7−x)13−2(x+1),then12L= , p. −2 If L=(lim)x→π4tan3x−tanxcos(x+π4),then−L4= , q. 2 If L=(lim)x→1(2x−3)(√x−1)2x2+x−3,then20L= , r. 1 If L=(lim)x→∞logxn−[x][x],wheren∈N,([x] denotes greatest integer less than or equal to x),then−2L= , s. −1
To solve the problem, we will analyze each limit statement in Column I and match it with the appropriate statement in Column II based on the calculations.
Step 1: Analyzing Statement A
Statement A:
L=limx→−1(7−x)1/3−2x+1
- Substitute x=−1:
L=(7−(−1))1/3−2−1+1=(8)1/3−20=2−20=00 (indeterminate form)
- Apply L'Hôpital's Rule:
- Derivative of the numerator:
13(7−x)−2/3⋅(−1)=−13(7−x)2/3
- Derivative of the denominator:
1
- Now, apply L'Hôpital's Rule:
L=limx→−1−13(7−x)2/3=−13(8)2/3=−13⋅4=−112
- Therefore, 12L=12⋅−112=−1.
Match: A matches with S (since 12L=−1).
Step 2: Analyzing Statement B
Statement B:
L=limx→π4tan3x−tanxcos(x+π4)
- Substitute x=π4:
L=tan3(π4)−tan(π4)cos(π4+π4)=1−10=00 (indeterminate form)
- Apply L'Hôpital's Rule:
- Derivative of the numerator:
3tan2xsec2x−sec2x
- Derivative of the denominator:
−sin(x+π4)
- Now, apply L'Hôpital's Rule:
L=limx→π4(3tan2x−1)sec2x−sin(x+π4)
- Substitute x=π4:
L=(3⋅1−1)⋅2−1=4−1=−4
- Therefore, −L4=−−44=1.
Match: B matches with R (since −L4=1).
Step 3: Analyzing Statement C
Statement C:
L=limx→1(2x−3)(√x−1)2x2+x−3
- Substitute x=1:
L=(2⋅1−3)(√1−1)2⋅12+1−3=(−1)(0)0=00 (indeterminate form)
- Apply L'Hôpital's Rule:
- Derivative of the numerator:
(2)(√x−1)+(2x−3)12√x
- Derivative of the denominator:
4x+1
- Now, apply L'Hôpital's Rule:
L=limx→1(2)(√x−1)+(2x−3)12√x4x+1
- Substitute x=1:
L=(2)(0)+(−1)124+1=−125=−110
- Therefore, 20L=20⋅−110=−2.
Match: C matches with P (since 20L=−2).
Step 4: Analyzing Statement D
Statement D:
L=limx→∞log(xn)−(x)(x)
- As x→∞, (x)≈x:
L=limx→∞nlogx−xx
- This simplifies to:
L=limx→∞(nlogxx−1)
- Since limx→∞logxx=0:
L=0−1=−1
- Therefore, −2L=−2⋅−1=2.
Match: D matches with Q (since −2L=2).
Summary of Matches
- A - S
- B - R
- C - P
- D - Q
Final Answer
The correctly bubbled 4 x 4 matrix should be:
- A matches with S
- B matches with R
- C matches with P
- D matches with Q
Statement A:
L=limx→−1(7−x)1/3−2x+1
- Substitute x=−1:
L=(7−(−1))1/3−2−1+1=(8)1/3−20=2−20=00 (indeterminate form)
- Apply L'Hôpital's Rule:
- Derivative of the numerator:
13(7−x)−2/3⋅(−1)=−13(7−x)2/3
- Derivative of the denominator:
1
- Now, apply L'Hôpital's Rule:
L=limx→−1−13(7−x)2/3=−13(8)2/3=−13⋅4=−112
- Therefore, 12L=12⋅−112=−1.
Statement B:
L=limx→π4tan3x−tanxcos(x+π4)
- Substitute x=π4:
L=tan3(π4)−tan(π4)cos(π4+π4)=1−10=00 (indeterminate form)
- Apply L'Hôpital's Rule:
- Derivative of the numerator:
3tan2xsec2x−sec2x
- Derivative of the denominator:
−sin(x+π4)
- Now, apply L'Hôpital's Rule:
L=limx→π4(3tan2x−1)sec2x−sin(x+π4)
- Substitute x=π4:
L=(3⋅1−1)⋅2−1=4−1=−4
- Therefore, −L4=−−44=1.
Statement C:
L=limx→1(2x−3)(√x−1)2x2+x−3
- Substitute x=1:
L=(2⋅1−3)(√1−1)2⋅12+1−3=(−1)(0)0=00 (indeterminate form)
- Apply L'Hôpital's Rule:
- Derivative of the numerator:
(2)(√x−1)+(2x−3)12√x
- Derivative of the denominator:
4x+1
- Now, apply L'Hôpital's Rule:
L=limx→1(2)(√x−1)+(2x−3)12√x4x+1
- Substitute x=1:
L=(2)(0)+(−1)124+1=−125=−110
- Therefore, 20L=20⋅−110=−2.
Statement D:
L=limx→∞log(xn)−(x)(x)
- As x→∞, (x)≈x:
L=limx→∞nlogx−xx
- This simplifies to:
L=limx→∞(nlogxx−1)
- Since limx→∞logxx=0:
L=0−1=−1
- Therefore, −2L=−2⋅−1=2.
- A - S
- B - R
- C - P
- D - Q
The correctly bubbled 4 x 4 matrix should be:
- A matches with S
- B matches with R
- C matches with P
- D matches with Q
Topper's Solved these Questions
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
- LINEAR INEQUALITIESBOOK - CENGAGE ENGLISHCHAPTER - LINEAR INEQUALITIESEXERCISE - All Questions
68 Videos
Similar Questions
Each question contains statements given in two columns which have to be matched . Statement (A,B,C,D) in column I have to be matched statements (p,q,r,s) in column II. Capillary rise and shape of droplets on a plate due to surface tension are shown in column - II . Match the following

View SolutionEach question contains statements given in two columns which have to be matched . Statement (A,B,C,D) in column I have to be matched statements (p,q,r,s) in column II. Capillary rise and shape of droplets on a plate due to surface tension are shown in column - II . Match the following

View SolutionEach question contains statements given in two columns which have to be matched. Statements a,b,c,d in column I have to be matched with statements p,q,r,s in column II. If the correct matches are a-p, q-s, b-q, r c-p, q and d-s, then the correctly bubbled 4x4 matrix should be as follows: Figure Column I, Column II: Differential equation order 1, p. of all parabolas whose axis is the x-axis order 2, q. of family of curves y=a(x+a)2, whre a is an arbitrary constant degree 1, r. (1+3dydx)23=4d3ydx3 degree 3, s. of family of curve y2=2c(x+√c), where c>0
View SolutionMatch the statement (A,B,C,D) in column I with the statement (p,q,r,s) in column II. The answers are to be properly bobbled.
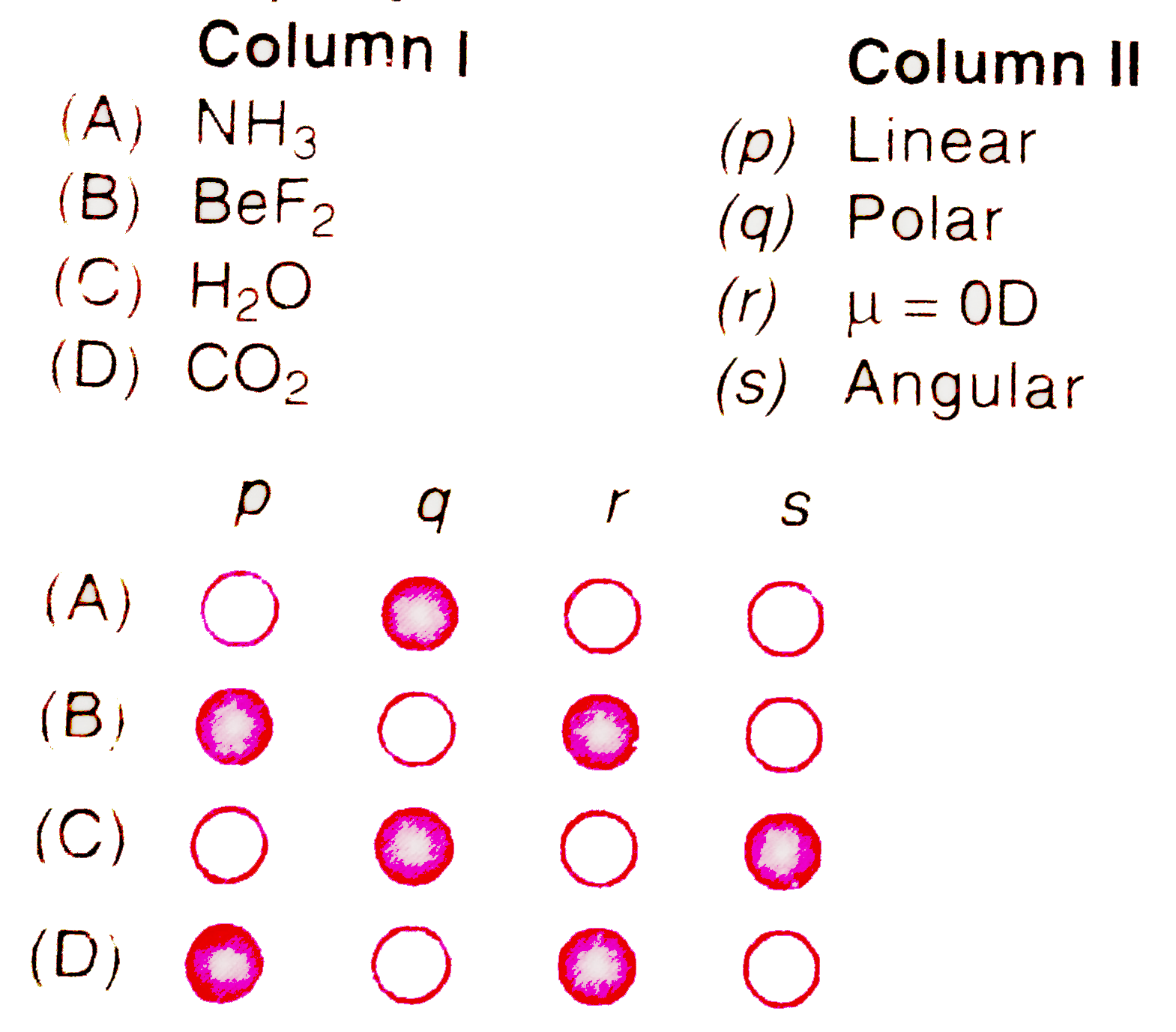
View SolutionMatch the statements (A, B, C, D) in Column I with the statements (p, q, r, s) in column II. The answers are to be properly bubbled.
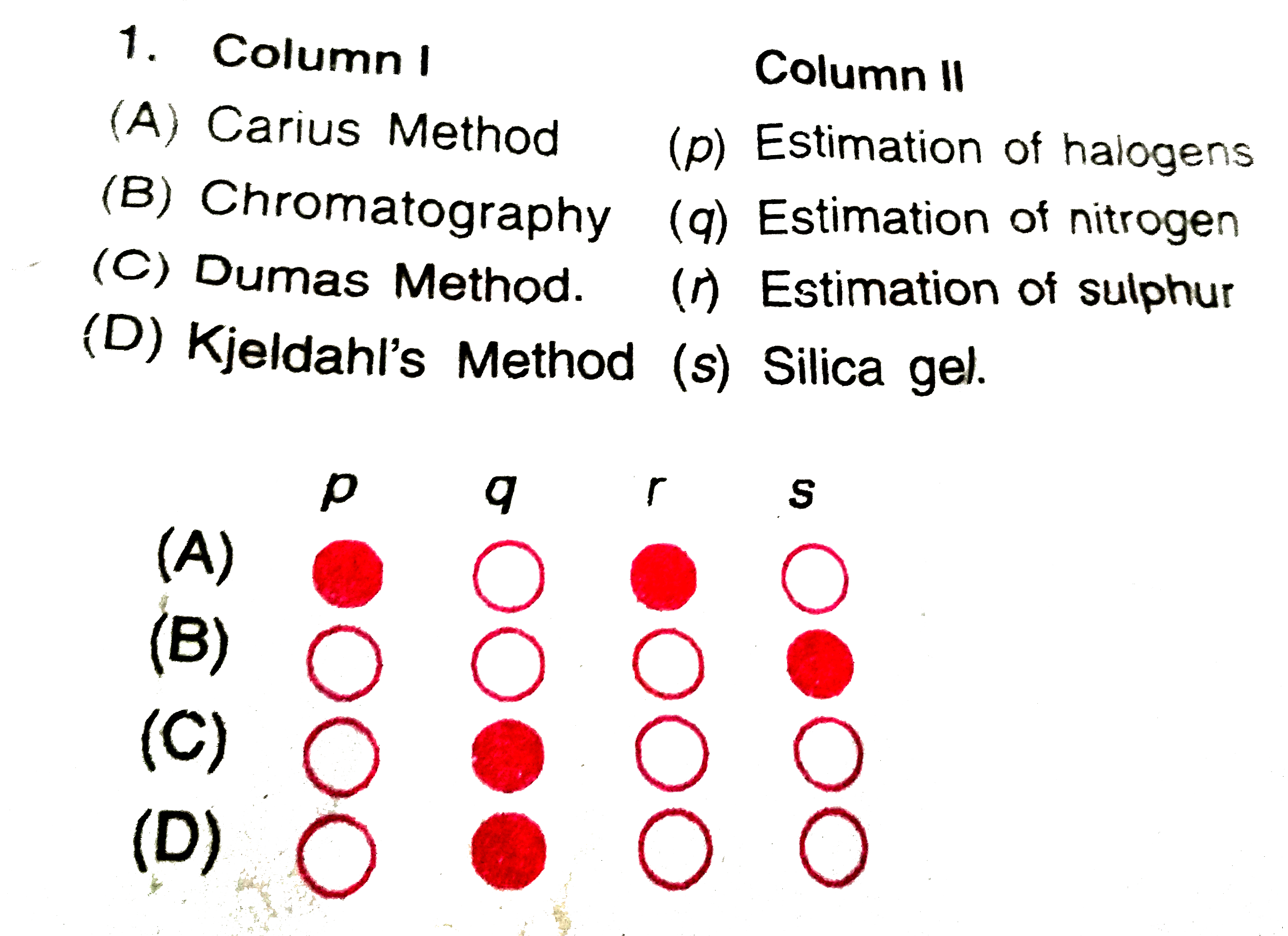
View SolutionEach question contains statements given in two columns which have to be matched. Statements (a,b,c,d) in column I have to be matched with statements (p,q,r,s) in column II. If the correct match are a-p, s, b-r c-p, q. and d-s, then the correctly bubbled 4x4 matrix should be as follows: figure Column I, a) If ∫2x√1−4xdx=ksin−1(f(x))+C, then kis greater than, b) If ∫(√x)5(√x)7+x6dx=aln(xk)xk+1+c, then akis less than, c) If ∫x4+1x(x2+1)2dx=kln|x|+m1+x2+n, where nis the constant of integration, then mkis greater than, d) If ∫dx5+4cosx=ktan−1(mtanx2)+C, then k/mis greater than, COLUMN II p) 0 q) 1 r) 3 s)4
View SolutionMatch the statement (A, B, C, D) in Column I with the statements (p, q, r, s) in Column II. The answer are to be properly bubbled.

View SolutionMatch the statement (A, B, C, D) in Column I with the statements (p, q, r, s) in Column II. The answer are to be properly bubbled.

View SolutionMatch the statement (A, B, C, D) in Column I with the statements (p, q, r, s) in Column II. The answer are to be properly bubbled.

View SolutionMatch the statement (A, B, C, D) in Column I with the statements (p, q, r, s) in Column II. The answer are to be properly bubbled.

View Solution
