Evaluate: (lim)x→0(ax+bx+cx3)2x;(a,b,c>0)
To evaluate the limit
limx→0(ax+bx+cx3)2x,(a,b,c>0)
we can follow these steps:
Step 1: Substitute the limit
First, we substitute x=0 into the expression:
a0+b0+c03=1+1+13=1
Thus, we have:
(ax+bx+cx3)2x→1∞ as x→0
Step 2: Apply the exponential limit property
Since we have an indeterminate form 1∞, we can use the property:
limx→af(x)g(x)=elimx→a(f(x)−1)g(x)
Here, let:
f(x)=ax+bx+cx3,g(x)=2x
Thus, we rewrite the limit:
limx→0(ax+bx+cx3)2x=elimx→0(ax+bx+cx3−1)⋅2x
Step 3: Simplify the expression inside the limit
Now we need to evaluate:
limx→0(ax+bx+cx3−1)⋅2x
This can be rewritten as:
limx→0ax+bx+cx−33⋅2x
Step 4: Use the Taylor expansion
Using the Taylor expansion for ax, bx, and cx around x=0:
ax≈1+xlna,bx≈1+xlnb,cx≈1+xlnc
Thus,
ax+bx+cx≈3+x(lna+lnb+lnc)
So,
ax+bx+cx−3≈x(lna+lnb+lnc)
Step 5: Substitute back into the limit
Substituting this back into our limit gives:
limx→0x(lna+lnb+lnc)3⋅2x=limx→02(lna+lnb+lnc)3
Step 6: Evaluate the limit
This limit evaluates to:
2(lna+lnb+lnc)3
Step 7: Final result
Now substituting this back into the exponential:
e2(lna+lnb+lnc)3=eln(a23b23c23)=(abc)23
Thus, the final result is:
limx→0(ax+bx+cx3)2x=(abc)23
First, we substitute x=0 into the expression:
Since we have an indeterminate form 1∞, we can use the property:
Now we need to evaluate:
Using the Taylor expansion for ax, bx, and cx around x=0:
Substituting this back into our limit gives:
This limit evaluates to:
Now substituting this back into the exponential:
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type11videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - LINEAR INEQUALITIESEXERCISE - All Questions68videos
LINEAR INEQUALITIES
Similar Questions
Evaluate: (lim)x→0sinx0x
View SolutionEvaluate: limx→0xx
View Solutionlimx→0(x3logx)
View SolutionThe value of limx→0{ax+bx+cx3}1/x, is
View SolutionEvaluate: limx→0tanx−sinxx3
View SolutionEvaluate limx→0(ax+bx+cx3)2/x,(a,b,c>0)
View SolutionEvaluate limx→0f(x), where
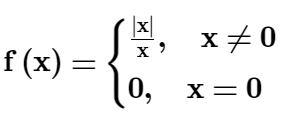 View Solution
View Solutionlimx→0xsecx
View SolutionEvaluate: limx→0sin5xtan3x.
View Solutionlimx→0ax+xcosxbsinx
View Solution

