If α=(z−i)(z+i), show that, when z lies above the real axis, α will lie within the unit circle which has center at the origin. Find the locus of αasz travels on the real axis from −∞→+∞.
To solve the problem, we need to show that when z lies above the real axis, α lies within the unit circle centered at the origin, and then find the locus of α as z travels along the real axis from −∞ to +∞.
1. Define α:
α=z−iz+i
2. Calculate the modulus of α:
|α|=∣∣∣z−iz+i∣∣∣=|z−i||z+i|
3. Express z:
Let z=x+iy, where y>0 (since z lies above the real axis).
4. Calculate |z−i| and |z+i|:
|z−i|=|x+i(y−1)|=√x2+(y−1)2
|z+i|=|x+i(y+1)|=√x2+(y+1)2
5. Substitute back into the modulus of α:
|α|=√x2+(y−1)2√x2+(y+1)2
6. Show that |α|<1:
We need to show:
√x2+(y−1)2<√x2+(y+1)2
Squaring both sides (since both sides are positive):
x2+(y−1)2<x2+(y+1)2
Simplifying gives:
(y−1)2<(y+1)2
Expanding both sides:
y2−2y+1<y2+2y+1
This simplifies to:
−2y<2y⟹0<4y⟹y>0
This is true since y>0. Thus, |α|<1 when z lies above the real axis, confirming that α lies within the unit circle.
7. Finding the locus of α:
Now, we need to find the locus of α as z travels along the real axis, where z=x (i.e., y=0):
α=x−ix+i
8. Calculate the modulus of α when y=0:
|α|=∣∣∣x−ix+i∣∣∣=|x−i||x+i|=√x2+1√x2+1=1
9. Express α in terms of x:
α=x−ix+i=(x−i)(x−i)(x+i)(x−i)=x2+1x2+1+−2ix2+1
This simplifies to:
α=1−2ix2+1
Letting α=x′+iy′, we have:
x′=1,y′=−2x2+1
10. Finding the locus:
As x varies from −∞ to +∞, y′ varies from 0 to −2. Therefore, the locus of α as z travels along the real axis is a vertical line segment from (1,0) to (1,−2).
α=z−iz+i
|α|=∣∣∣z−iz+i∣∣∣=|z−i||z+i|
Let z=x+iy, where y>0 (since z lies above the real axis).
|z−i|=|x+i(y−1)|=√x2+(y−1)2
|z+i|=|x+i(y+1)|=√x2+(y+1)2
|α|=√x2+(y−1)2√x2+(y+1)2
We need to show:
√x2+(y−1)2<√x2+(y+1)2
Squaring both sides (since both sides are positive):
x2+(y−1)2<x2+(y+1)2
Simplifying gives:
(y−1)2<(y+1)2
Expanding both sides:
y2−2y+1<y2+2y+1
This simplifies to:
−2y<2y⟹0<4y⟹y>0
This is true since y>0. Thus, |α|<1 when z lies above the real axis, confirming that α lies within the unit circle.
Now, we need to find the locus of α as z travels along the real axis, where z=x (i.e., y=0):
α=x−ix+i
|α|=∣∣∣x−ix+i∣∣∣=|x−i||x+i|=√x2+1√x2+1=1
α=x−ix+i=(x−i)(x−i)(x+i)(x−i)=x2+1x2+1+−2ix2+1
This simplifies to:
α=1−2ix2+1
Letting α=x′+iy′, we have:
x′=1,y′=−2x2+1
As x varies from −∞ to +∞, y′ varies from 0 to −2. Therefore, the locus of α as z travels along the real axis is a vertical line segment from (1,0) to (1,−2).
Topper's Solved these Questions
Similar Questions
If α=(z−i)/(z+i) show that, when z lies above the real axis, αwill lie within the unit circle which has centre at the origin. Find the locus of α as z travels on the real axis form −∞to+∞
View SolutionIf z≠1 and z2z−1 is real, then the point represented by the complex number z lies (1) either on the real axis or on a circle passing through the origin (2) on a circle with centre at the origin (3) either on the real axis or on a circle not passing through the origin (4) on the imaginary axis
View SolutionIf z≠1 and z2z−1 is real, then the point represented by the complex number z lies (1) either on the real axis or on a circle passing through the origin (2) on a circle with centre at the origin (3) either on the real axis or on a circle not passing through the origin (4) on the imaginary axis
View SolutionFind the equation of the circle which lies in the first quadrant and touching each-co ordinate-axis at a distance of 2 units from the origin.
View SolutionFind the equation to the circles which pass through the origin and cut off intercepts equal to (i) 3 and 4, (ii) 2a and 2b from the x-axis and the y-axis respectively.
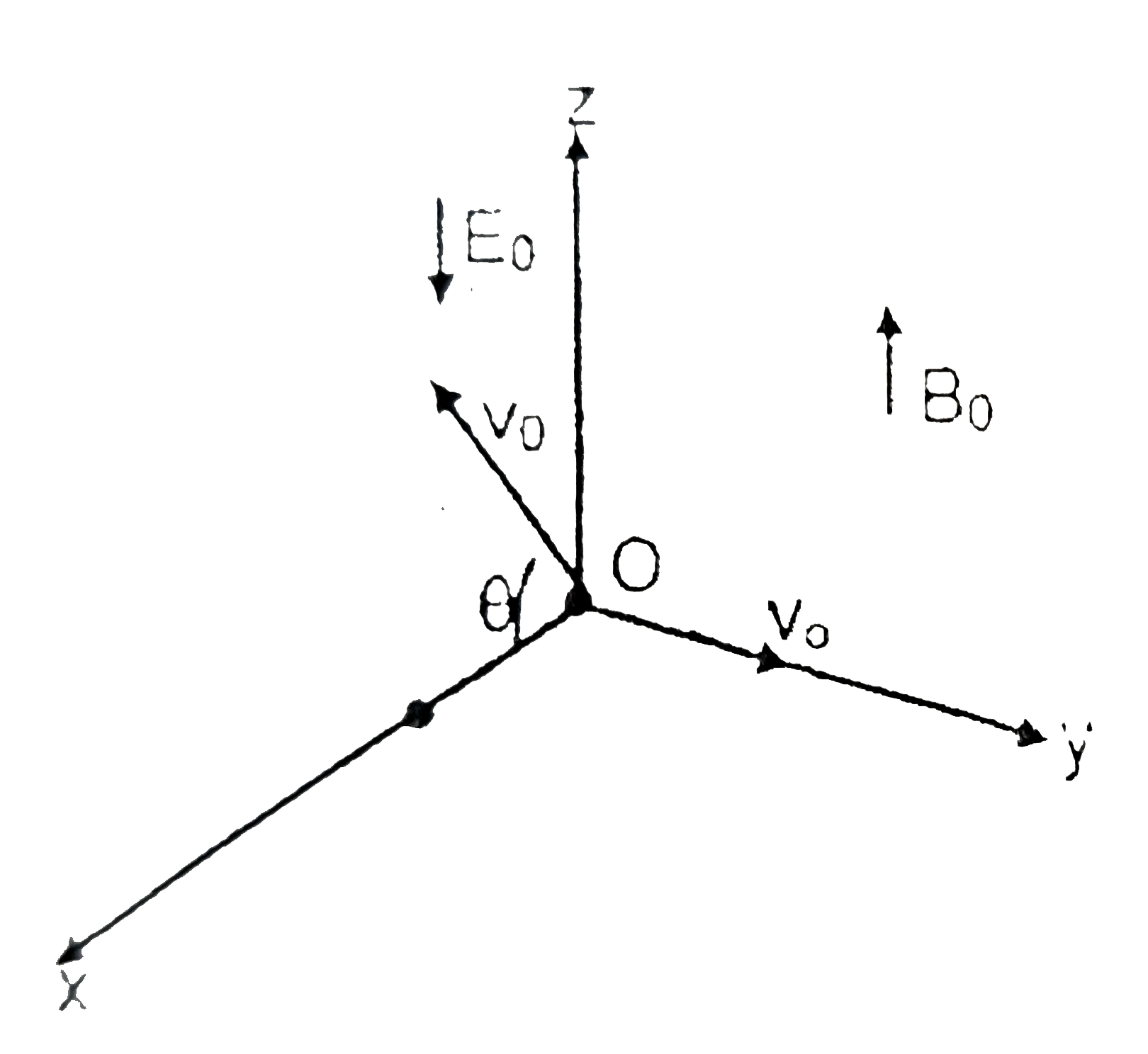
View SolutionA charged point particle having positive charge q, mass m is projected in x−z plane with a speed v0 at an angle θ with the x−axis , while another identical particle is projected simultaneously along the y−axis from the origin (see figure) with an equal speed v0.
An electric field →E=−E0ˆk exists in the x−z plane, while a magnetic field →B=B0ˆk exists in the region y>0 (F0, B0>0). It is observed that both the particles collide after some time. Assume that the space is gravity free.
(i) Find the time after which the particles collide and the coordinates of the point of collision.
(ii) Find the velocity v0 and the angle θ in terms of the other variables.
(iii) What is the maximum value of the z− coordinate of the first particle ?
View SolutionA circular ring of radius R with uniform positive charge density λ per unit length is located in the y z plane with its center at the origin O. A particle of mass m and positive charge q is projected from that point p(−√3R,0,0) on the negative x - axis directly toward O, with initial speed V. Find the smallest (nonzero) value of the speed such that the particle does not return to P ?
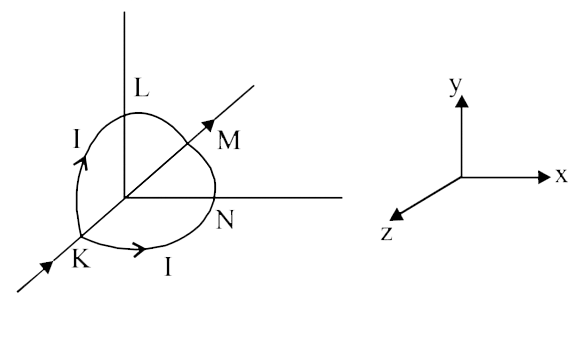
View SolutionA circular loop of radius R is bent along a diameter and given a shapes as shown in the figure. One of the semicircles (KNM) lies in the x−z plane with their centres and the other one (KLM) in the y−z plane with their centres at the origin. current I is flowing through each of the semi circles as shown in figure.
(a) A particle of charge q is released at the origin with a velocity →v=−v0ˆi. Find the instantaneous force →F on the particle . Assume that space is gravity free.
(b) If an external uniform magnetic field B0ˆj is applied , determine the force →F1and→F2 on the semicircles KLMandKNM due to the field and the net force →F on the loop.
View SolutionFind the range of real number α for which the equation z+α|z−1|+2i=0 has a solution.
View SolutionFind the range of real number α for which the equation z+α|z−1|+2i=0 has a solution.
View Solution
