Two towns A and B are 60 km a part. A school is to be built to serve 150 students in town A and 50 students in town B. If the total distance to be travelled by all 200 students is to be as small as possible, then the school be built be (a) town B (b) 45 k from town A (c) town A (d) 45 km from town B
To solve the problem, we need to determine the optimal location for a school to minimize the total distance traveled by students from towns A and B.
1. Identify the Distance Between Towns:
- The distance between towns A and B is given as 60 km.
2. Define Variables:
- Let x be the distance from town A to the school.
- Therefore, the distance from town B to the school will be 60−x.
3. Calculate Total Distance Traveled:
- There are 150 students in town A and 50 students in town B.
- The total distance traveled by all students can be expressed as:
Total Distance=(150×x)+(50×(60−x))
4. Simplify the Expression:
- Expanding the equation:
Total Distance=150x+3000−50x
- Combining like terms:
Total Distance=100x+3000
5. Minimize the Total Distance:
- The expression 100x+3000 is linear in terms of x.
- To minimize this distance, we need to consider the endpoints of the interval for x (0 to 60 km).
- Since the coefficient of x is positive, the minimum distance occurs at the smallest value of x, which is x=0.
6. Determine the Location of the School:
- If x=0, the school is located at town A.
- Therefore, the optimal location for the school is at town A.
Conclusion:
The school should be built in town A.
Answer:
(c) town A
- The distance between towns A and B is given as 60 km.
- Let x be the distance from town A to the school.
- Therefore, the distance from town B to the school will be 60−x.
- There are 150 students in town A and 50 students in town B.
- The total distance traveled by all students can be expressed as:
Total Distance=(150×x)+(50×(60−x))
- Expanding the equation:
Total Distance=150x+3000−50x
- Combining like terms:
Total Distance=100x+3000
- The expression 100x+3000 is linear in terms of x.
- To minimize this distance, we need to consider the endpoints of the interval for x (0 to 60 km).
- Since the coefficient of x is positive, the minimum distance occurs at the smallest value of x, which is x=0.
- If x=0, the school is located at town A.
- Therefore, the optimal location for the school is at town A.
The school should be built in town A.
(c) town A
Topper's Solved these Questions
Similar Questions
Two towns AandB are 60 km apart. A school is to be built to serve 150 students in town Aand50 students in town B. If the total distance to be travelled by 200 students is to be as small as possible, then the school should be built at (a)town B (b)town A (c)45 km from town A (d)45 km from town B
View Solution45% of the students in a school are boys. If the total number of students in the school is 880, find the number of girls in the school.
View Solution
Knowledge Check
In a school assembly, students are asked to stand in rows. 6 students stand in the first row, 8 students in the second row, 10 students in the third row and so on.
If there are total of 150 students, then the total number of rows formed is:A8B9C10D11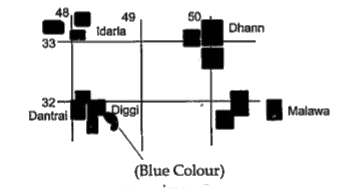
Which is the most important town in th above image ?AIdarlaBMalawaCDantraiDDhann
Find the mean age of 100 residents of a town from the following data.

View SolutionThe distance between the school and the house of a student is 1km 875m. Everyday she walks both ways between her school and home. Find the total distance covered by her in a week.
View SolutionA school collected Rs 2304 as fees from its students. If each student paid as many paise as there were students in the school, how many students were there in the school ?
View SolutionThe annual fee charged from a student of class VI in a school is Rs. 8880. If there are, in all, 235 students in class VI, find the total collection.
View SolutionIn a school there are two sections section A and section B of class X . There are 32 students in section A and 36 students in section B . Determine the minimum number of books required for their class library so that they can be distributed equally among students of section A or section B .
View SolutionOn a rainy day, 94% of the students were present in a school. If the number of students absent on that day was 174, find the total strength of the school.
View Solution
