Match the following for the equation is a parameter. Column I, Column II No real roots, p. Two real roots, q. Three real roots, r. Four distinct real roots, s.
To solve the problem, we need to analyze the equation x2+a|x|+1=0 for different values of the parameter a and determine the nature and number of roots. We will categorize the roots based on the conditions given in the question.
1. Identify the Equation: The given equation is:
x2+a|x|+1=0
2. Case 1: a≥0:
- When a is non-negative, the term a|x| is always non-negative.
- Thus, the equation can be rewritten as:
x2+a|x|+1≥0
- This implies that the left-hand side is always positive or zero, meaning there are no real roots.
- Therefore, we match this case with:
- No real roots corresponds to s (i.e., a≥0).
3. Case 2: a=−2:
- Substitute a=−2 into the equation:
x2−2|x|+1=0
- This can be factored as:
(|x|−1)2=0
- Thus, |x|−1=0 gives us two real roots:
x=1andx=−1
- Therefore, we match this case with:
- Two real roots corresponds to r (i.e., a=−2).
4. Case 3: a<−2:
- For a<−2, we analyze the discriminant of the quadratic equation:
x2+a|x|+1=0
- The discriminant D must be calculated for the quadratic:
D=(a|x|)2−4⋅1⋅1=a2−4
- For the quadratic to have real roots, we require:
a2−4>0⟹|a|>2
- Since a<−2, this condition holds true, and we can find that there are four distinct real roots.
- Therefore, we match this case with:
- Four distinct real roots corresponds to p (i.e., a<−2).
5. Case 4: −2<a<0:
- In this range, we can analyze the roots using the quadratic formula:
x=−b±√D2a
- The discriminant will be positive, indicating that there are two real roots.
- However, since we already matched a=−2 with two real roots, we do not have a case for three real roots in this equation.
- Therefore, we conclude that:
- Three real roots does not apply in this case.
Final Matching
- No real roots: a≥0 matches with s.
- Two real roots: a=−2 matches with r.
- Four distinct real roots: a<−2 matches with p.
- Three real roots: does not apply.
Summary of Matches
- No real roots: s (for a≥0)
- Two real roots: r (for a=−2)
- Four distinct real roots: p (for a<−2)
- Three real roots: does not match any condition.
x2+a|x|+1=0
- When a is non-negative, the term a|x| is always non-negative.
- Thus, the equation can be rewritten as:
x2+a|x|+1≥0
- This implies that the left-hand side is always positive or zero, meaning there are no real roots.
- Therefore, we match this case with:
- No real roots corresponds to s (i.e., a≥0).
- Substitute a=−2 into the equation:
x2−2|x|+1=0
- This can be factored as:
(|x|−1)2=0
- Thus, |x|−1=0 gives us two real roots:
x=1andx=−1
- Therefore, we match this case with:
- Two real roots corresponds to r (i.e., a=−2).
- For a<−2, we analyze the discriminant of the quadratic equation:
x2+a|x|+1=0
- The discriminant D must be calculated for the quadratic:
D=(a|x|)2−4⋅1⋅1=a2−4
- For the quadratic to have real roots, we require:
a2−4>0⟹|a|>2
- Since a<−2, this condition holds true, and we can find that there are four distinct real roots.
- Therefore, we match this case with:
- Four distinct real roots corresponds to p (i.e., a<−2).
- In this range, we can analyze the roots using the quadratic formula:
x=−b±√D2a
- The discriminant will be positive, indicating that there are two real roots.
- However, since we already matched a=−2 with two real roots, we do not have a case for three real roots in this equation.
- Therefore, we conclude that:
- Three real roots does not apply in this case.
- No real roots: a≥0 matches with s.
- Two real roots: a=−2 matches with r.
- Four distinct real roots: a<−2 matches with p.
- Three real roots: does not apply.
- No real roots: s (for a≥0)
- Two real roots: r (for a=−2)
- Four distinct real roots: p (for a<−2)
- Three real roots: does not match any condition.
Topper's Solved these Questions
Similar Questions
Match the following for the equation x2+a|x|+1=0 where, a is a parameter.

View SolutionMatch the following column I with column II :

View SolutionMatch the following Column I with column II:

View SolutionMatch the following columns I with column II.

View SolutionMatch the following (Column I with Column II)
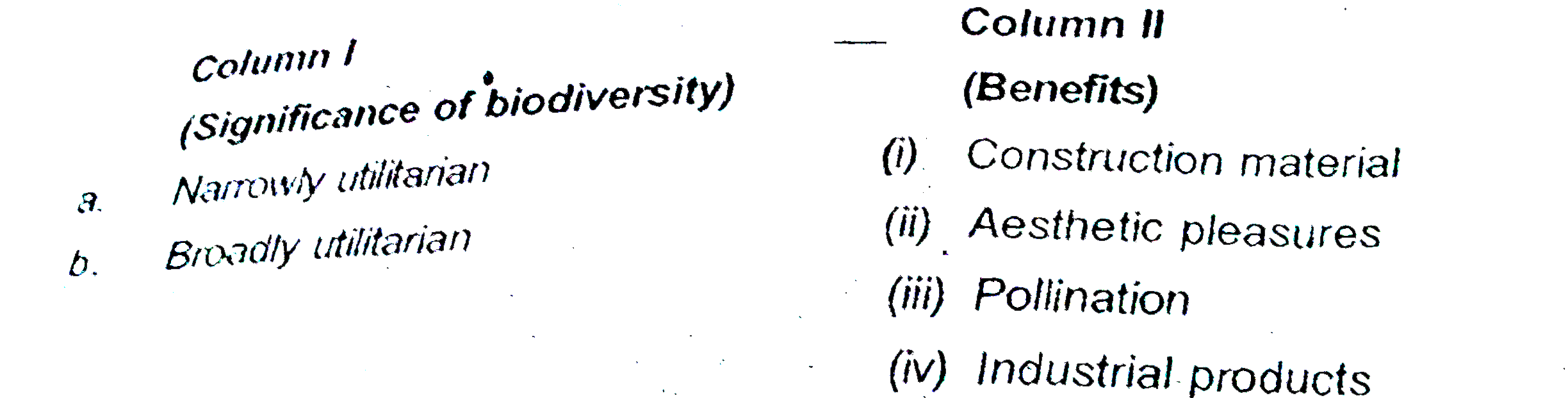
View SolutionMatch the following column I with column-II :
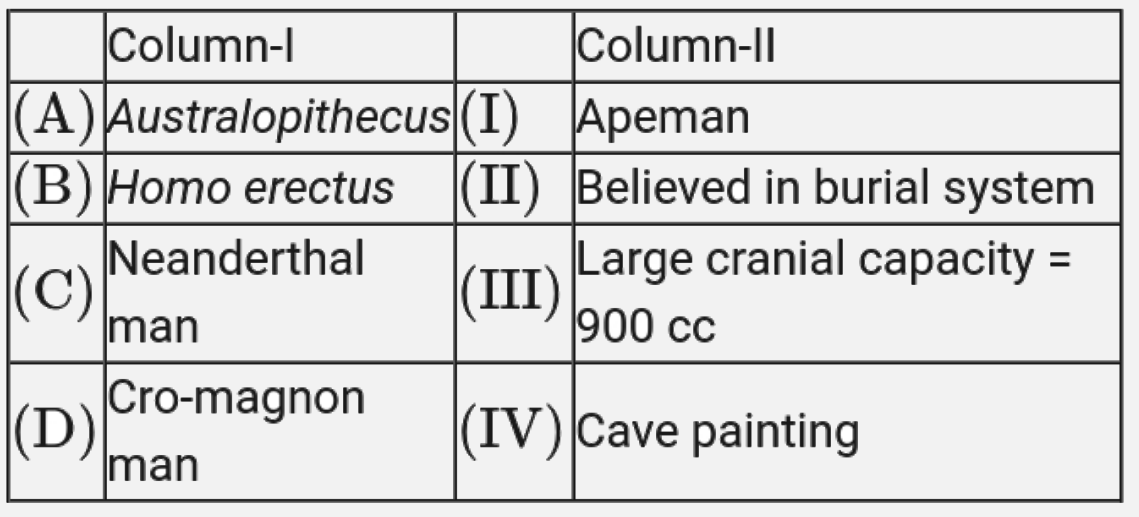
View SolutionMatch the following (Column I with Column II).

View SolutionMatch the following Column I with Column II
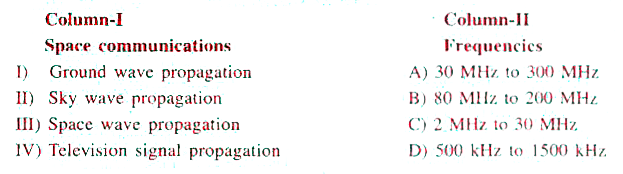
Code
View SolutionMatch the following (column-I with column-II)

View SolutionMatch the following (column-I with column-II)
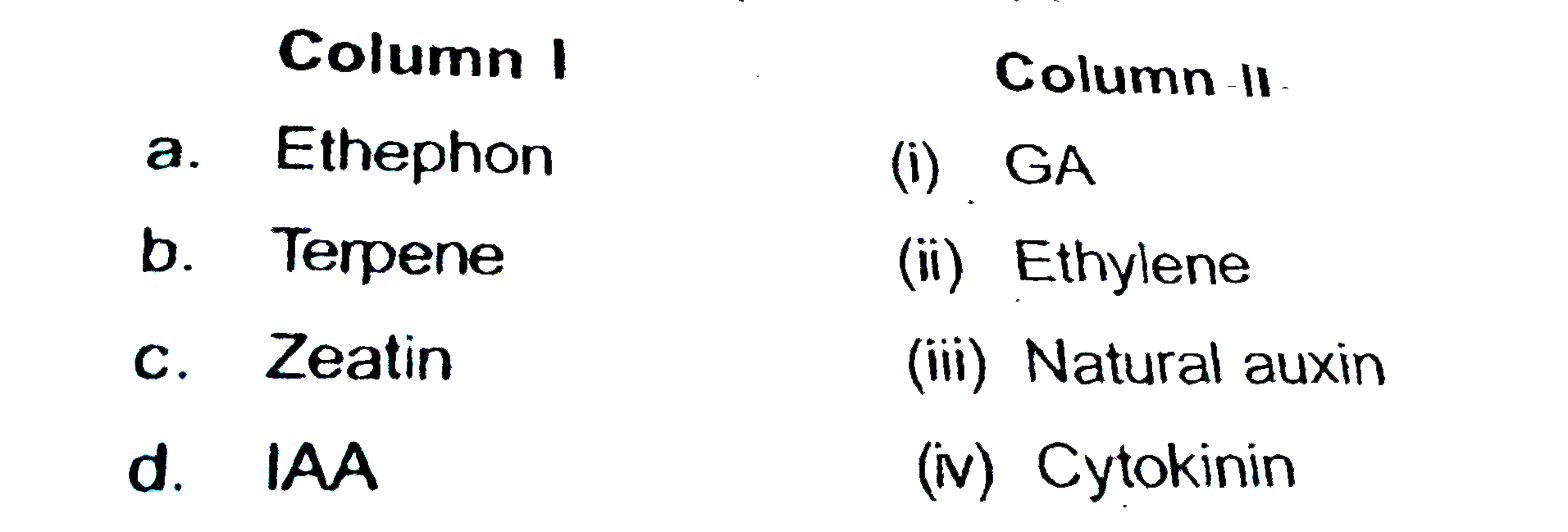
View Solution
