m equi spaced horizontal lines are intersection by n equi spaced vertical lines. If the distance between two successive horizontal lines is same as that between two successive vertical lines, then find the number of squares formed by lines if (m
To find the number of squares formed by m equi-spaced horizontal lines intersected by n equi-spaced vertical lines, we can follow these steps:
1. Understanding the Grid:
We have m horizontal lines and n vertical lines. The lines create a grid of intersections. The distance between successive horizontal lines is equal to the distance between successive vertical lines.
2. Identifying the Size of Squares:
A square can be formed by selecting a starting point (top-left corner) and extending downwards and to the right. The size of the square can vary from 1x1 up to the maximum possible square that can fit within the grid.
3. Calculating Squares of Size 1x1:
The number of 1x1 squares that can be formed is given by the number of positions where the top-left corner of the square can be placed. This is:
\(
(m-1) \times (n-1)
\)
This is because the top-left corner can be placed anywhere in the first m−1 horizontal lines and the first n−1 vertical lines.
4. Calculating Squares of Size 2x2:
For 2x2 squares, the top-left corner can be placed in the first m−2 horizontal lines and the first n−2 vertical lines:
\(
(m-2) \times (n-2)
\)
5. Continuing this Pattern:
We can continue this process for squares of size kxk, where k can range from 1 to min(m−1,n−1). The number of kxk squares is given by:
\(
(m-k) \times (n-k)
\)
6. Summing Up All Possible Squares:
The total number of squares can be calculated by summing the squares of all possible sizes:
\(
\text{Total Squares} = \sum_{k=1}^{\min(m-1, n-1)} (m-k)(n-k)
\)
7. Final Formula:
This can be expressed as:
\(
\text{Total Squares} = (m-1)(n-1) + (m-2)(n-2) + (m-3)(n-3) + \ldots + (1)(1)
\)
Conclusion:
Thus, the total number of squares formed by m horizontal lines and n vertical lines is given by the above summation.
We have m horizontal lines and n vertical lines. The lines create a grid of intersections. The distance between successive horizontal lines is equal to the distance between successive vertical lines.
A square can be formed by selecting a starting point (top-left corner) and extending downwards and to the right. The size of the square can vary from 1x1 up to the maximum possible square that can fit within the grid.
The number of 1x1 squares that can be formed is given by the number of positions where the top-left corner of the square can be placed. This is:
\(
(m-1) \times (n-1)
\)
This is because the top-left corner can be placed anywhere in the first m−1 horizontal lines and the first n−1 vertical lines.
For 2x2 squares, the top-left corner can be placed in the first m−2 horizontal lines and the first n−2 vertical lines:
\(
(m-2) \times (n-2)
\)
We can continue this process for squares of size kxk, where k can range from 1 to min(m−1,n−1). The number of kxk squares is given by:
\(
(m-k) \times (n-k)
\)
The total number of squares can be calculated by summing the squares of all possible sizes:
\(
\text{Total Squares} = \sum_{k=1}^{\min(m-1, n-1)} (m-k)(n-k)
\)
This can be expressed as:
\(
\text{Total Squares} = (m-1)(n-1) + (m-2)(n-2) + (m-3)(n-3) + \ldots + (1)(1)
\)
Thus, the total number of squares formed by m horizontal lines and n vertical lines is given by the above summation.
Topper's Solved these Questions
Similar Questions
m equi spaced horizontal lines are inersected by n equi spaced vertical lines. If the distance between two successive horizontal lines is same as that between two successive vertical lines, then find the number of squares formed by the lines if (m<n)
View SolutionThe phase between the two successive M phase is called as
View Solution
Knowledge Check
An area between two Z lines forms
AA bandBI bandCH bandDsarcomere
The contractie element present in the myofibril of a striated muscle between two successive Z-lines is called
View SolutionIf the angle between two lines regression is 90∘, then it represents
View SolutionIf the angle between two lines is π4and slope of one of the lines is 12, find the slope of the other line.
View SolutionIf two lines intersect prove that the vertically opposite angles are equal
View SolutionThe flat horizontal line in between the waves of ECG represent time when
View Solution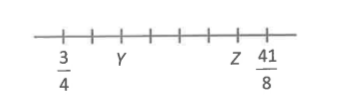
If the tick marks on the number line above are evenly spaced, what is the distnace, between Y and Z?
View SolutionThe area between two Z lines is called a …………....
View Solution
