The distance covered by a particle moving in a straight line from a fixed point on the line is where Then prove that acceleration is proportional to
To prove that the acceleration a is proportional to s−3 given the equation s2=at2+2bt+c, we will follow these steps:
Step 1: Start with the given equation
We have:
s2=at2+2bt+c
Step 2: Differentiate s2 with respect to time t
Using the chain rule:
d(s2)dt=2sdsdt
Differentiating the right-hand side:
ddt(at2+2bt+c)=2at+2b
Setting the derivatives equal gives:
2sdsdt=2at+2b
Dividing both sides by 2:
sdsdt=at+b
Step 3: Solve for dsdt
Rearranging gives:
dsdt=at+bs
Step 4: Differentiate dsdt to find acceleration
Now we differentiate dsdt with respect to t:
d2sdt2=ddt(at+bs)
Using the quotient rule:
d2sdt2=sddt(at+b)−(at+b)dsdts2
Calculating ddt(at+b):
ddt(at+b)=a
Substituting this into the equation gives:
d2sdt2=s⋅a−(at+b)⋅at+bss2
This simplifies to:
d2sdt2=as−(at+b)2ss2
Step 5: Simplify the expression for acceleration
Combining the terms:
d2sdt2=as2−(at+b)2s3
Thus, the acceleration a is given by:
a=as2−(at+b)2s3
Step 6: Show that acceleration is proportional to s−3
Since a=as2−(at+b)2s3, we can express this as:
a∝1s3
This shows that acceleration is indeed proportional to s−3.
Conclusion
We have proved that the acceleration a is proportional to s−3.
We have:
s2=at2+2bt+c
Using the chain rule:
d(s2)dt=2sdsdt
Differentiating the right-hand side:
ddt(at2+2bt+c)=2at+2b
Setting the derivatives equal gives:
2sdsdt=2at+2b
Dividing both sides by 2:
sdsdt=at+b
Rearranging gives:
dsdt=at+bs
Now we differentiate dsdt with respect to t:
d2sdt2=ddt(at+bs)
Using the quotient rule:
d2sdt2=sddt(at+b)−(at+b)dsdts2
Calculating ddt(at+b):
ddt(at+b)=a
Substituting this into the equation gives:
d2sdt2=s⋅a−(at+b)⋅at+bss2
This simplifies to:
d2sdt2=as−(at+b)2ss2
Combining the terms:
d2sdt2=as2−(at+b)2s3
Thus, the acceleration a is given by:
a=as2−(at+b)2s3
Since a=as2−(at+b)2s3, we can express this as:
a∝1s3
This shows that acceleration is indeed proportional to s−3.
We have proved that the acceleration a is proportional to s−3.
Similar Questions
The distance covered by a particle moving in a straight line from a fixed point on the line is s, where s2=at2+2bt+c. Then prove that acceleration is proportional to s−3.
View SolutionIf the velocity v of a particle moving along a straight line and its distance s from a fixed point on the line are related by v2=a2+s2, then its acceleration equals
View SolutionThe distance travelled by a particle in a straight line motion is directly proportional to t1/2, where t is the time elapsed.
View SolutionA particle moves in a straight line so that s=√t, then its acceleration is proportional to
View SolutionA particle moves in a straight line so that s=√t, then its acceleration is proportional to
View SolutionThe space s described in time t by a particle moving in a straight line is given by s=t5−40t3+30t2+80t−250 . Find the minimum value of acceleration.
View SolutionIf a particle moves along a line by S=√1+t then its acceleration is proportional to
View SolutionThe velovity-time graph of a particle moving in a straitht line is shown in . The acceleration of the particle at t=9s is.
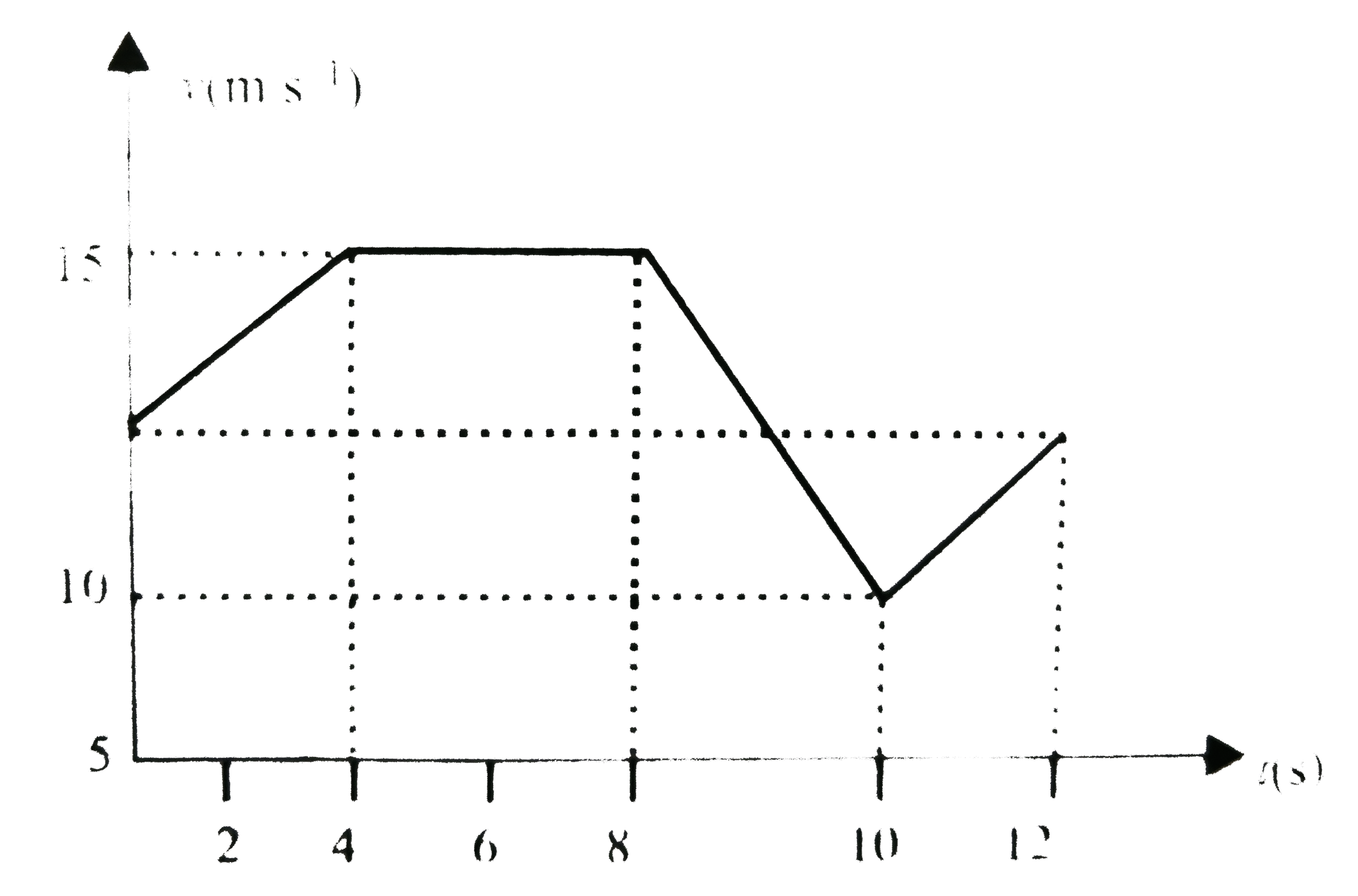 .
.
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View SolutionThe displacement of a particle moving in a straight line is described by the relation s=6+12t−2t2. Here s is in metre and t in second. The distance covered by the particle in first 5s is
View Solution
