Using the relation $2 (1 - cos x)$ < $x^{2}$ , $x = 0$ or prove that $sin (tan x) \geq x, \forall ϵ [0, \frac{π}{4}]$

Video Solution

|

Answer

Step by step video & image solution for Using the relation 2(1−cosx)<x^2 ,x=0 or prove that sin(tanx)≥x,∀ϵ[0,π/4] by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF DERIVATIVES

Similar Questions

The number of solutions of the equation $\frac{sec x}{1 - cos x} = \frac{1}{1 - cos x}$ in $[0, 2 π]$ is equal to 3 (b) 2 (c) 1 (d) 0
View Solution
Solutions of the equations $(2 cos x - 1) (3 cos x + 4) = 0$ is $[0, 2 π]$ is:
View Solution
Integrate the functions $\frac{1 - cos x}{1 + cos x}$
View Solution
Integrate the functions $\frac{cos x}{1 + cos x}$
View Solution
Using constraint method find the relation between of $a_{1}$ and $a_{2}$ .

View Solution
Using constraint method find the relation between accelerations of $1$ and $2$ .

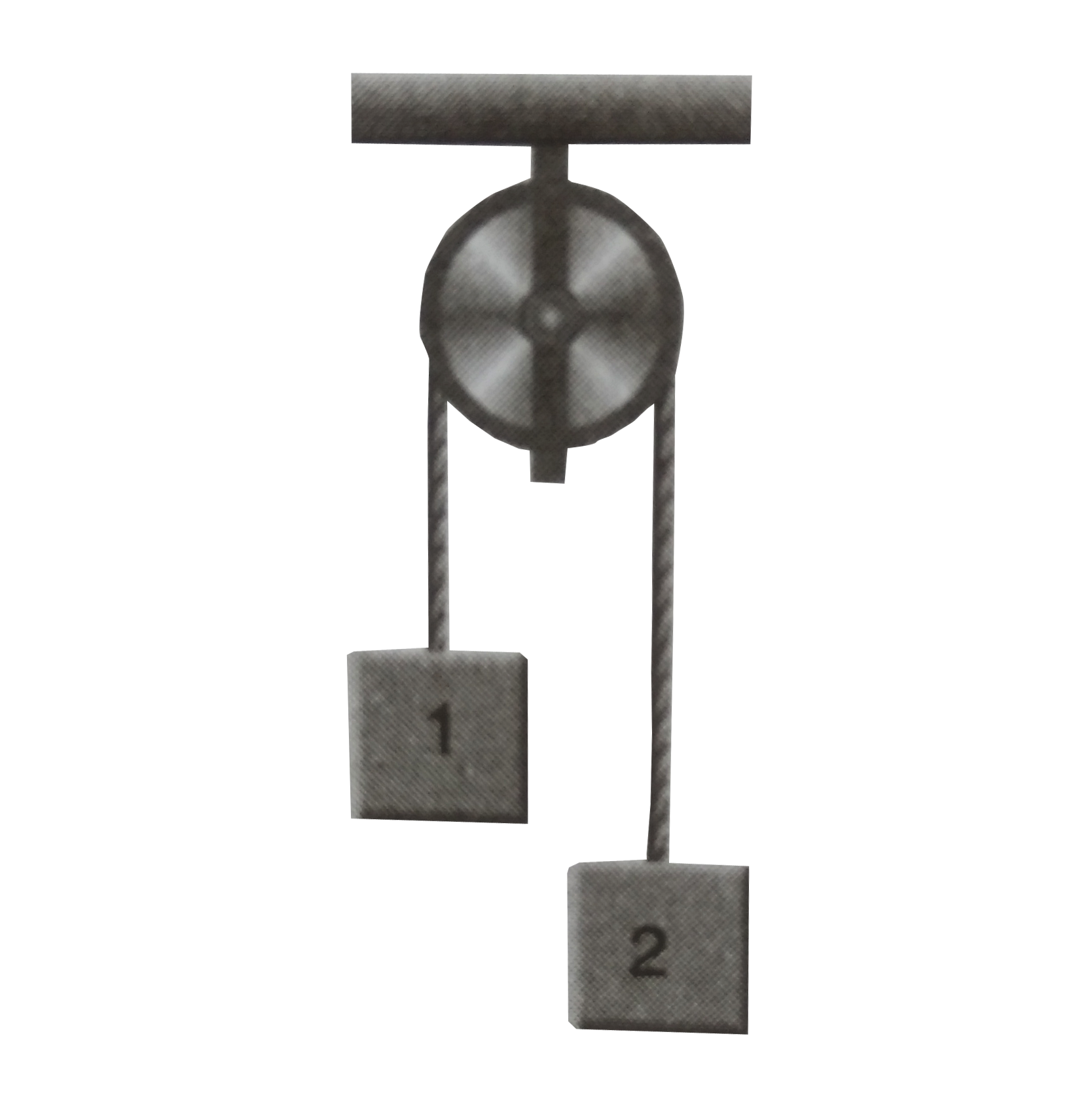
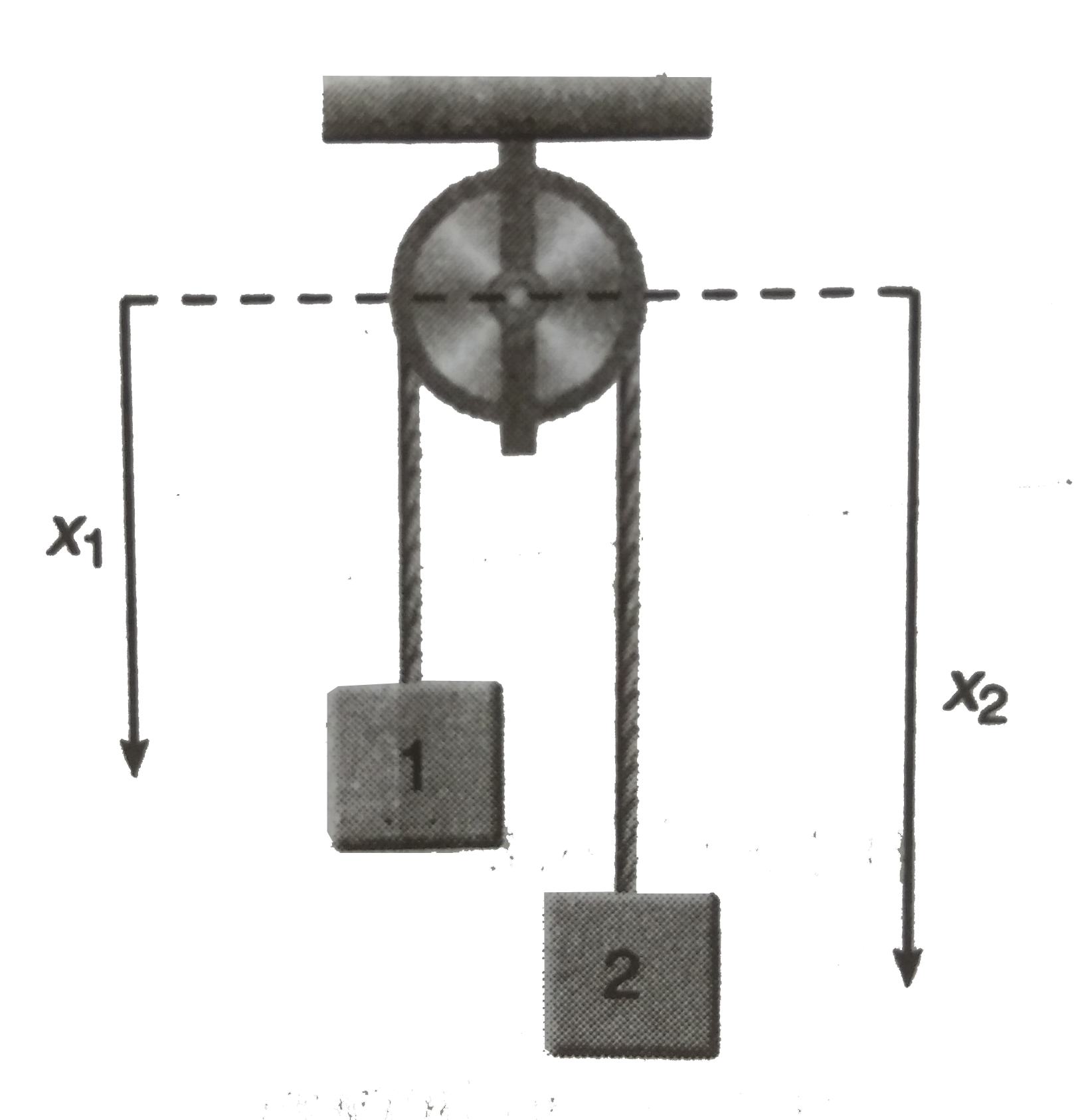
View Solution
Using contraint equation. Find the relation between $a_{1} and a_{2} .$

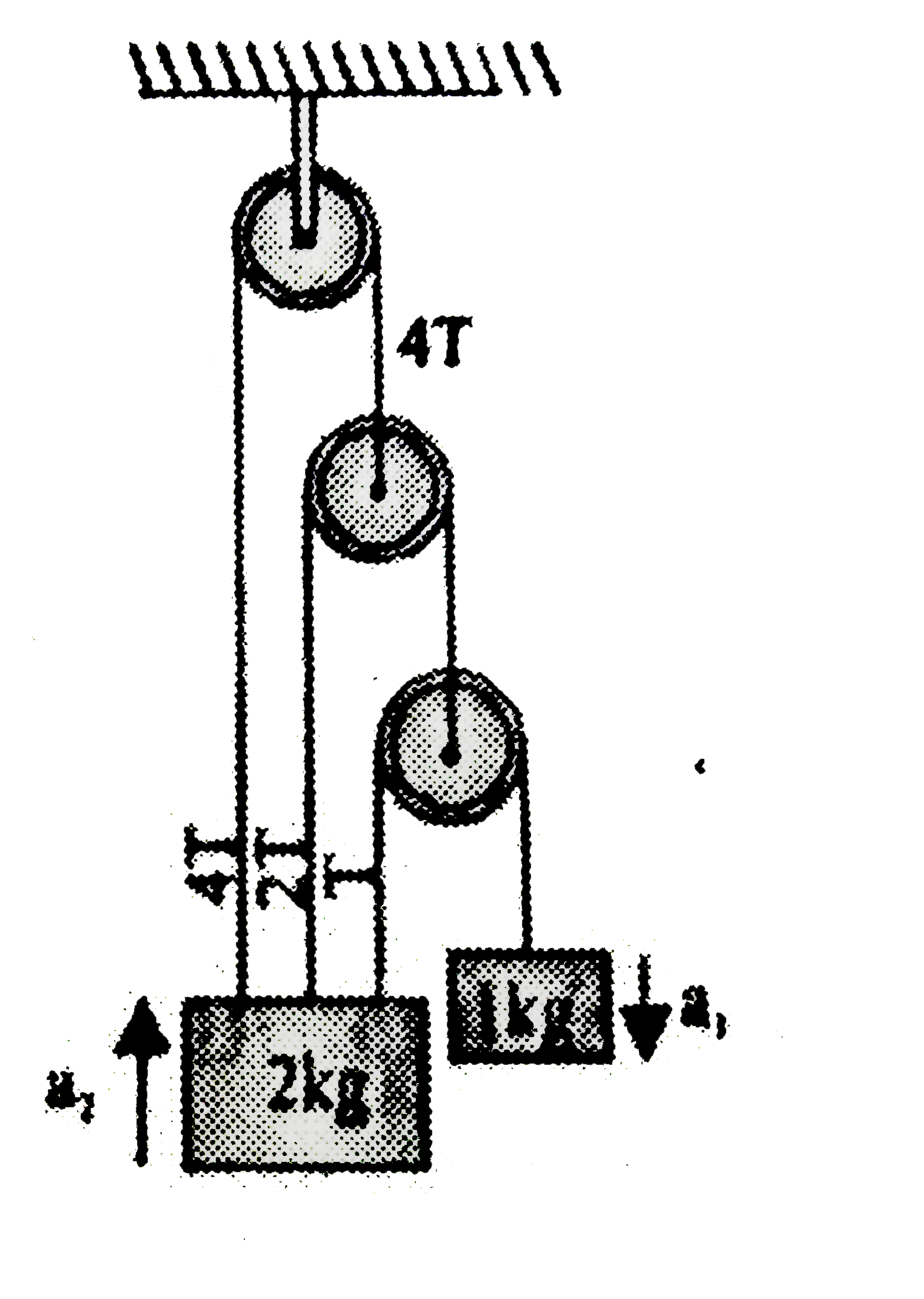
View Solution
Find the solution of $cos x = \frac{1}{2}$ .
View Solution
If $x_{1}, x_{2}, ..., x_{n}$ are real numbers, then the largest value of the expression
${sin x}_{1} {cos x}_{2} + {sin x}_{2} {cos x}_{3} + ... + {sin x}_{n} {cos x}_{1},$ is
View Solution
solve equation $2 {tan}^{- 1} (cos x) = {tan}^{- 1} (2 cos e c x)$
View Solution

Using the relation 2(1−cosx)<x2 ,x=0 or prove that sin(tanx)≥x,∀ϵ[0,π4]

Similar Questions

Recommended Questions

Using the relation $2 (1 - cos x)$ < $x^{2}$ , $x = 0$ or prove that $sin (tan x) \geq x, \forall ϵ [0, \frac{π}{4}]$