f:R→R,f(x) is differentiable such that f(f(x))=k(x5+x),k≠0). Then f(x) is always increasing (b) decreasing either increasing or decreasing non-monotonic
To solve the problem, we need to analyze the function f(f(x))=k(x5+x) and determine the monotonicity of f(x).
Step 1: Differentiate the given function
We start by differentiating both sides of the equation f(f(x))=k(x5+x).
Using the chain rule, we have:
ddx(f(f(x)))=f′(f(x))⋅f′(x)
On the right-hand side, we differentiate k(x5+x):
ddx(k(x5+x))=k(5x4+1)
So, we can equate the derivatives:
f′(f(x))⋅f′(x)=k(5x4+1)
Step 2: Analyze the expression
Now, we need to analyze the expression k(5x4+1).
1. The term 5x4+1 is always positive for all x because 5x4≥0 and adding 1 ensures it is greater than 0.
2. Therefore, the sign of k(5x4+1) depends solely on the sign of k.
Step 3: Determine the implications of k
- If k>0:
- Then k(5x4+1)>0.
- This implies f′(f(x))⋅f′(x)>0.
- Since f′(f(x)) is a function of f(x) and f′(x) is a function of x, both must have the same sign. Therefore, f′(x)>0 for all x, meaning f(x) is increasing.
- If k<0:
- Then k(5x4+1)<0.
- This implies f′(f(x))⋅f′(x)<0.
- This means f′(x) and f′(f(x)) have opposite signs. Therefore, f′(x)<0 for all x, meaning f(x) is decreasing.
Conclusion
Since k can either be positive or negative, we conclude that f(x) is either increasing (if k>0) or decreasing (if k<0). Thus, the correct answer is:
Either increasing or decreasing.
---
We start by differentiating both sides of the equation f(f(x))=k(x5+x).
ddx(f(f(x)))=f′(f(x))⋅f′(x)
On the right-hand side, we differentiate k(x5+x):
ddx(k(x5+x))=k(5x4+1)
f′(f(x))⋅f′(x)=k(5x4+1)
Now, we need to analyze the expression k(5x4+1).
2. Therefore, the sign of k(5x4+1) depends solely on the sign of k.
- If k>0:
- Then k(5x4+1)>0.
- This implies f′(f(x))⋅f′(x)>0.
- Since f′(f(x)) is a function of f(x) and f′(x) is a function of x, both must have the same sign. Therefore, f′(x)>0 for all x, meaning f(x) is increasing.
- Then k(5x4+1)<0.
- This implies f′(f(x))⋅f′(x)<0.
- This means f′(x) and f′(f(x)) have opposite signs. Therefore, f′(x)<0 for all x, meaning f(x) is decreasing.
Since k can either be positive or negative, we conclude that f(x) is either increasing (if k>0) or decreasing (if k<0). Thus, the correct answer is:
Similar Questions
The function f(x)=x2−x+1 is increasing and decreasing in the intervals
View SolutionIf f(x)=xex(x−1), then f(x) is
View SolutionIf f(x)=xex(x−1) , then f(x) is
View SolutionThe function f(x)=x1+|x| is (a) strictly increasing (b) strictly decreasing (c) neither increasing nor decreasing (d) none of these
View SolutionState whether f(x)=tanx−x is increasing or decreasing its domain.
View SolutionFor each of the following graphs, comment whether f(x) is increasing or decreasing or neither increasing nor decreasing at x = a.
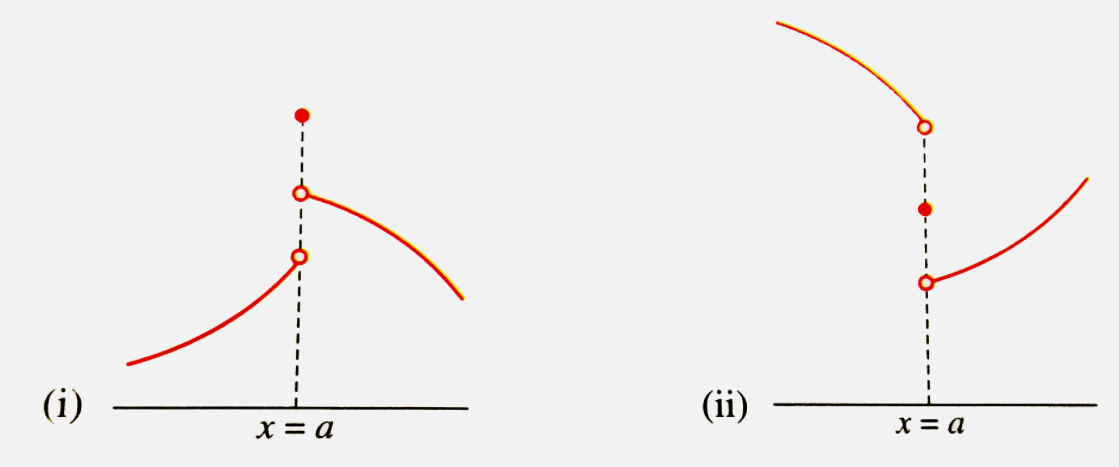
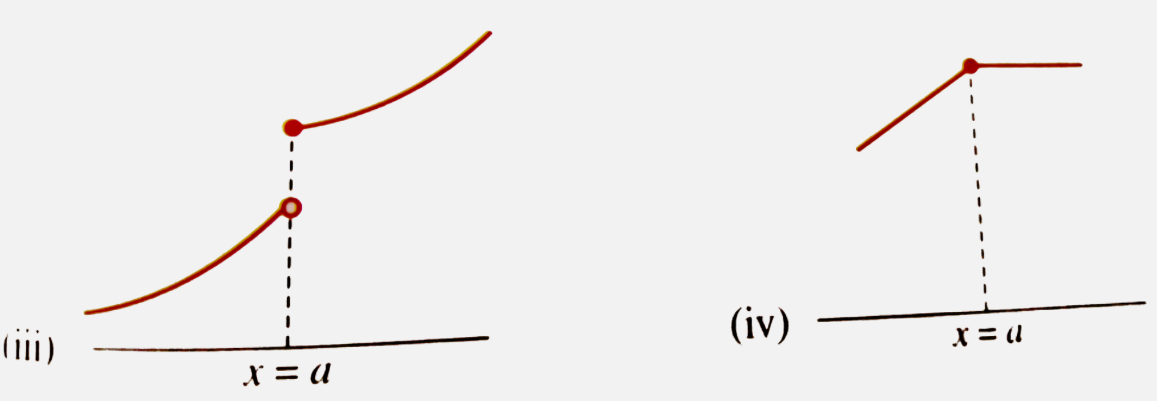
View SolutionFind the intervals in which f(x)=xlogx is increasing or decreasing
View SolutionFind the interval for which f(x)=x−sinx is increasing or decreasing.
View SolutionFind the intervals in which f(x)=xlogx is increasing or decreasing.
View SolutionShow that f(x)=cosx is decreasing function on (0,π), increasing in (−π,0) and neither increasing nor decreasing in (−π,π).
View Solution
