Without expanding the determinants, prove that ∣∣ ∣∣103115114111108106104113116∣∣ ∣∣+∣∣ ∣∣113116104108106111115114103∣∣ ∣∣=0
To prove that
|∣∣
∣∣103115114111108106104113116∣∣
∣∣|+|∣∣
∣∣113116104108106111115114103∣∣
∣∣|=0
we will denote the first determinant as A1 and the second determinant as A2. We will manipulate A2 using row and column operations without expanding the determinants.
Step 1: Interchange Columns
First, we interchange the first and third columns of A2:
A2=|∣∣
∣∣104116113111106108103114115∣∣
∣∣|
Interchanging two columns introduces a negative sign:
A2=−|∣∣
∣∣104116113111106108103114115∣∣
∣∣|
Step 2: Interchange Rows
Next, we interchange the first and third rows of A2:
A2=−|∣∣
∣∣103116113104106108111114115∣∣
∣∣|
Again, interchanging two rows introduces another negative sign:
A2=|∣∣
∣∣103116113104106108111114115∣∣
∣∣|
Step 3: Interchange Columns Again
Now, we interchange the second and third columns of A2:
A2=|∣∣
∣∣103113116104108106111115114∣∣
∣∣|
This again introduces a negative sign:
A2=−|∣∣
∣∣103113116104108106111115114∣∣
∣∣|
Step 4: Rearranging to Match A1
Now, we can see that the resulting matrix after the operations is a rearrangement of the original matrix A1:
A2=−|∣∣
∣∣103115114111108106104113116∣∣
∣∣|
Conclusion
Thus, we have:
A2=−A1
Now substituting back into the original equation:
A1+A2=A1−A1=0
Therefore, we conclude that:
|∣∣
∣∣103115114111108106104113116∣∣
∣∣|+|∣∣
∣∣113116104108106111115114103∣∣
∣∣|=0
∣∣103115114111108106104113116∣∣
∣∣|+|∣∣
∣∣113116104108106111115114103∣∣
∣∣|=0
First, we interchange the first and third columns of A2:
∣∣104116113111106108103114115∣∣
∣∣|
∣∣104116113111106108103114115∣∣
∣∣|
Next, we interchange the first and third rows of A2:
∣∣103116113104106108111114115∣∣
∣∣|
∣∣103116113104106108111114115∣∣
∣∣|
Now, we interchange the second and third columns of A2:
∣∣103113116104108106111115114∣∣
∣∣|
∣∣103113116104108106111115114∣∣
∣∣|
Now, we can see that the resulting matrix after the operations is a rearrangement of the original matrix A1:
∣∣103115114111108106104113116∣∣
∣∣|
Thus, we have:
∣∣103115114111108106104113116∣∣
∣∣|+|∣∣
∣∣113116104108106111115114103∣∣
∣∣|=0
Topper's Solved these Questions
- DETERMINANTBOOK - CENGAGE ENGLISHCHAPTER - DETERMINANTEXERCISE - Multiple Correct Answer
5 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
Without expanding, prove that Δ=∣∣ ∣ ∣∣x+yy+zz+xzxy111∣∣ ∣ ∣∣=0
View SolutionFind the value of the determinant ∣∣ ∣∣101102103104105106107108109∣∣ ∣∣
View SolutionThe weights in grams of 50 oranges picked at random from a consignment are as follows: 131, 113, 82, 75, 204, 81, 84, 118, 104, 110, 80, 107, 111, 141, 136, 123, 90, 78, 90, 115, 110, 98, 106, 99, 107, 84, 76, 186, 82, 100, 109, 128, 115, 107, 115, 119, 93, 187, 139, 129, 130, 68, 195, 123, 125, 111, 92, 86, 70, 126
View SolutionThe minimum temperature (in ∘C) during the day at Delhi has been recorded for 30 days, as given below:
11.8,11.6,11.6,11.4,11.3,11.4,
11.7,11.7,11.3,11.4,11.7,11.7,
11.6,11.3,11.5,11.8,11.3,
11.3,11.4,11.5,11.3,11.5,11.5,
11.8,11.5,11.4,11.3,11.6,11.5
Construct a frequency table for the above data.
View SolutionThe weights in grams of 50 oranges picked at random from a consignment are as follows: 131,113,82,75,204,81,84,118,104,110,80,107,111,141, 136,123,90,78,90,115,110,98,106,99,107,84,76,186,82, 100,109,128,115,107,115,119,93,187,139,129,130,68, 195,123,125,111,92,86,70,126 Form the grouped frequency table by dividing the variable range into intervals of equal width, each corresponding to 20gms in such a way that the mid-value of the first class corresponds to 70 gms.
View SolutionFrom the prices of shares X and Y below, find out which is more stable in value X 35 54 52 53 56 58 52 50 51 49 . Y 108 107 105 105 106 107 104 103 104 101
View SolutionFrom the prices of shares X and Y given below: find out which is more stable value: X: 35 54 52 53 56 58 52 50 50 49 Y: 108 107 105 105 106 107 104 103 104 101
View SolutionWhich of the following is correct:
(a) The element Mendelebium (d) has been named is the honour of Mendeleev. What is the atomic number of that element?
(i) 100 , (ii) 101 , (iii) 102 , (iv) 103
(b) The element Seaborgium (Sg) has been nemed in the honour of Glenn T. Seaborg. What is the atomic number of that elements?
(i) 104 , (ii) 105 , (iii) 106 , (iv) 107
(c ) Glenn T. Seaborg was awarded Nobel Prize in 1951 for the discovery of which element/elements?
(i) Uranium (U)
(ii) Elelments from 90 to 93
(iii) Elements from 94 to 102
(iv) elements from 103 to 106
View SolutionFollowing is the distribution of I.Q. of 100 students. Find the median I.Q. I.Q.55-64 65-74 75-84 85-94 95-104 105-114 115-124 125-134 135-144 No. of Students: 1 2 9 22 33 22 8 2 1
View SolutionA meter bridge is set- up as shown in figure, to determine an unknown resistance X using a standard 10Ω resistor. The galvanometer shows null point when tapping - key is at 52cm mark. The end -corrections are 1m and 2cm respectively for the ends A and B. The determined values of X is .
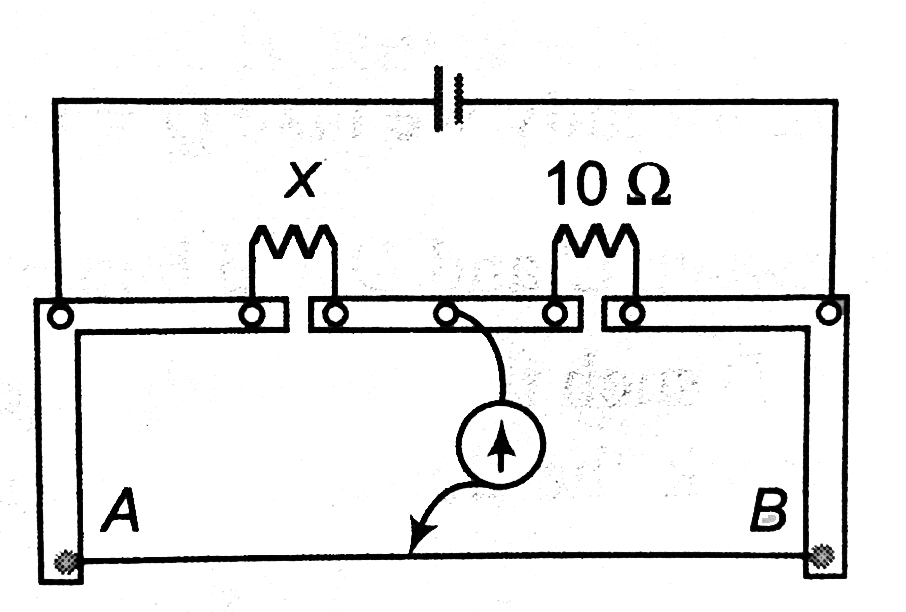
(a) 10.2Omeaga
(b) 10.6Ω
(c) 10.8Ω
(d) 11.1Ω.
View Solution
