Three distinct points and are collinear then is equal to
To solve the problem of determining the value of uv+vw+wu given that the points P(3u2,2u3), Q(3v2,2v3), and R(3w2,2w3) are collinear, we can follow these steps:
Step 1: Set Up the Determinant
To check if the points are collinear, we can use the determinant of the matrix formed by the coordinates of the points. The points can be represented as follows:
P=(3u2,2u3),Q=(3v2,2v3),R=(3w2,2w3)
We can set up the determinant:
∣∣
∣
∣∣3u22u313v22v313w22w31∣∣
∣
∣∣=0
Step 2: Calculate the Determinant
Calculating the determinant, we can expand it as follows:
=3u2∣∣∣2v312w31∣∣∣−2u3∣∣∣3v213w21∣∣∣+1∣∣∣3v22v33w22w3∣∣∣
Calculating the 2x2 determinants:
1. ∣∣∣2v312w31∣∣∣=2v3⋅1−2w3⋅1=2(v3−w3)
2. ∣∣∣3v213w21∣∣∣=3v2⋅1−3w2⋅1=3(v2−w2)
3. ∣∣∣3v22v33w22w3∣∣∣=3v2⋅2w3−2v3⋅3w2=6v2w3−6v3w2=6v2w2(v−w)
Substituting these back into the determinant:
=3u2⋅2(v3−w3)−2u3⋅3(v2−w2)+6v2w2(v−w)
Step 3: Factor and Simplify
Using the identities v3−w3=(v−w)(v2+vw+w2) and v2−w2=(v−w)(v+w):
=6u2(v−w)(v2+vw+w2)−6u3(v−w)(v+w)+6v2w2(v−w)
Factoring out (v−w):
=(v−w)(6u2(v2+vw+w2)−6u3(v+w)+6v2w2)
Setting the determinant to zero gives us the condition for collinearity:
6u2(v2+vw+w2)−6u3(v+w)+6v2w2=0
Step 4: Conclusion
Since P,Q,R are distinct points, we can conclude that:
uv+vw+wu=0
Final Answer
Thus, the value of uv+vw+wu is:
0
To check if the points are collinear, we can use the determinant of the matrix formed by the coordinates of the points. The points can be represented as follows:
∣
∣∣3u22u313v22v313w22w31∣∣
∣
∣∣=0
Calculating the determinant, we can expand it as follows:
Using the identities v3−w3=(v−w)(v2+vw+w2) and v2−w2=(v−w)(v+w):
Since P,Q,R are distinct points, we can conclude that:
Thus, the value of uv+vw+wu is:
Topper's Solved these Questions
- DETERMINANTBOOK - CENGAGE ENGLISHCHAPTER - DETERMINANTEXERCISE - Multiple Correct Answer
5 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
Knowledge Check
(3+ω+3ω2)4=λω, then value of λ is :
A4B−4C16D−820u3v6(2)−15u2v10u4v+30u3v3
Which of the following is the reduced form of the expression above?A5uv40u7v4B2v−1u+2uv2C4uv−32u2+2uv2D2uv−3uv2u2+6
If A=⎛⎜⎝100210321⎞⎟⎠,U1,U2,andU3 are column matrices
satisfying AU1=⎛⎜⎝100⎞⎟⎠,AU2=⎛⎜⎝230⎞⎟⎠andAU3=⎛⎜⎝231⎞⎟⎠ and
U is 3×3 matrix when columns areU1,U2,U3 then
answer the following questions
The value of (3 2 0) U⎛⎜⎝320⎞⎟⎠ is
View SolutionStatement 1 : The chord of contact of the circle x2+y2=1 w.r.t. the points (2, 3), (3, 5), and (1, 1) are concurrent. Statement 2 : Points (1, 1), (2, 3), and (3, 5) are collinear.
View SolutionLet a,b,c and d are real numbers in GP. Suppose u,v,w satisfy the system of equations u+2v+3w=6,4u+5v+6w=12 and 6u+9v=4. Further consider the expressions
f(x)=(1u+1v+1w)x2+[(b−c)2+(c−a)2+(x−b)2]
x+u+v+w=0 and g(x)=20x2+10(a−d)2x−9=0
(u+v+w) is equal to
View SolutionFig shows three resistor configuration R1,R2andR3 connected to 3V battery. If the power dissipated by the configuration R1,R2andR3 is P1,P2andP3 respectively, then
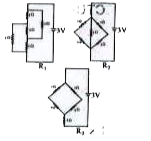
View SolutionIf each pair of the three equations x2−p1x+q1=0,x2−p2c+q2=0,x2−p3x+q3=0 have common root, prove that, p21+p22+p23+4(q1+q2+q3)=2(p2p3+p3p1+p1p2)
View SolutionIf 3u+w=7 and 3k-9u=2, what is the value of w+k?
View Solution
