The area enclosed by f(x)=12+ax−x2 coordinates axes and the ordinates at x=3(f(3)>0) is 45 sq. units. If mandn are the x-axis intercepts of the graph of y=f(x), then the value of (m+n+a) is____
To solve the problem step by step, we need to find the area enclosed by the function f(x)=12+ax−x2, the coordinate axes, and the ordinates at x=3. Given that this area is equal to 45 square units, we will find the values of m, n, and a and then compute m+n+a.
Step 1: Set up the integral for the area
The area A under the curve from x=0 to x=3 is given by the integral:
A=∫30f(x)dx=∫30(12+ax−x2)dx
We know that this area equals 45 square units:
∫30(12+ax−x2)dx=45
Step 2: Calculate the integral
Now we calculate the integral:
∫(12+ax−x2)dx=12x+a2x2−13x3
Evaluating this from 0 to 3:
(12x+a2x2−13x3)30=(12(3)+a2(32)−13(33))−0
Calculating this gives:
=36+a2(9)−13(27)=36+9a2−9
Thus,
=27+9a2
Step 3: Set up the equation
Setting the area equal to 45:
27+9a2=45
Subtracting 27 from both sides:
9a2=18
Multiplying both sides by 2:
9a=36
Dividing by 9:
a=4
Step 4: Find the x-intercepts (m and n)
Now substituting a=4 back into the function:
f(x)=12+4x−x2
To find the x-intercepts, set f(x)=0:
−x2+4x+12=0
Rearranging gives:
x2−4x−12=0
Using the quadratic formula x=−b±√b2−4ac2a:
x=4±√(−4)2−4(1)(−12)2(1)=4±√16+482=4±√642=4±82
Calculating the roots:
1. x=122=6 (let's call this n)
2. x=−42=−2 (let's call this m)
Thus, we have:
- m=−2
- n=6
Step 5: Calculate m+n+a
Now we can find m+n+a:
m+n+a=−2+6+4=8
Final Answer
The value of m+n+a is 8.
The area A under the curve from x=0 to x=3 is given by the integral:
A=∫30f(x)dx=∫30(12+ax−x2)dx
We know that this area equals 45 square units:
∫30(12+ax−x2)dx=45
Now we calculate the integral:
∫(12+ax−x2)dx=12x+a2x2−13x3
Evaluating this from 0 to 3:
(12x+a2x2−13x3)30=(12(3)+a2(32)−13(33))−0
Calculating this gives:
=36+a2(9)−13(27)=36+9a2−9
Thus,
=27+9a2
Setting the area equal to 45:
27+9a2=45
Subtracting 27 from both sides:
9a2=18
Multiplying both sides by 2:
9a=36
Dividing by 9:
a=4
Now substituting a=4 back into the function:
f(x)=12+4x−x2
To find the x-intercepts, set f(x)=0:
−x2+4x+12=0
Rearranging gives:
x2−4x−12=0
Using the quadratic formula x=−b±√b2−4ac2a:
x=4±√(−4)2−4(1)(−12)2(1)=4±√16+482=4±√642=4±82
Calculating the roots:
1. x=122=6 (let's call this n)
2. x=−42=−2 (let's call this m)
- m=−2
- n=6
Now we can find m+n+a:
m+n+a=−2+6+4=8
The value of m+n+a is 8.
Topper's Solved these Questions
Similar Questions
The area enclosed by f(x)=12+ax±x2 coordinates axes and the ordinates at x=3(f(3)>0) is 45 sq. units. If m and n are the x-axis intercepts of the graph of y=f(x), then the value of (m+n+a) si ___.
View SolutionThe area bounded by the curve y=f(x) the coordinate axes and the line x = t is given by tet then f(x) =
View Solution
Knowledge Check
The graph of y=f(x) is shown in the standard (x,y) coordinate plane below with points V,W,X,Y,and Z labeled .
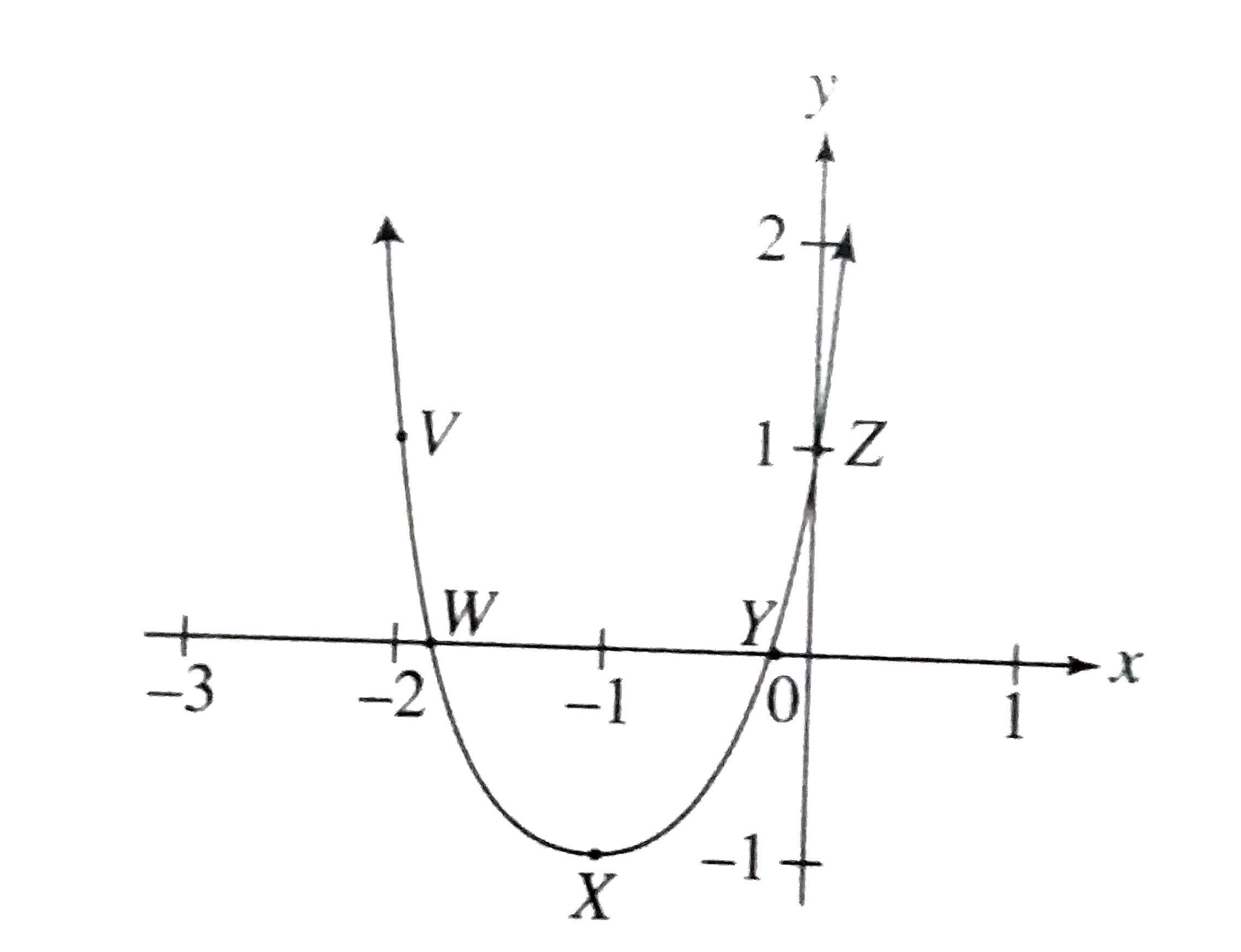
The y- intercept of the graph of y=f(x) is located at which of the following points ?AVBWCXDZSuppose the graph of f(x)=−x3+2 is translated 2 units right and 3 units down. If the result is the graph of Y=g(x), what is the value of g(-1.2)?
 A-33.77B-1.51C-0.49D31.77
A-33.77B-1.51C-0.49D31.77
If f(x)=2x3+mx2−13x+n and 2 and 3 are 2 roots of the equations f(x)=0, then values of m and n are
View SolutionIf f(x)=2x3+mx2−13x+n and 2 and 3 are 2 roots of the equations f(x)=0, then values of m and n are
View SolutionIf the area bounded by the curve f(x)=x13(x−1) and the x-axis is A, then the value of 28A is____
View SolutionThe ratio between masses of two planets is 3 : 5 and the ratio between their radii is 5 : 3. The ratio between their acceleration due to gravity will be
View SolutionThe area (in sq. units) enclosed by the graphs of |x+y|=2and|x|=1 is
View SolutionLet f(x)=(x−1)(x−2)(x−3)−−(x−n),n∈N,andf(n)=5040. Then the value of n is________
View Solution
