If the vertices P, Q, R of a triangle PQR are rational points, which of the following points of the triangle POR is (are) always rational point(s) ?
To determine which points of triangle PQR are always rational when the vertices P, Q, and R are rational points, we will analyze the properties of the triangle and its associated points.
1. Identify the Coordinates of the Vertices:
Let the vertices of triangle PQR be represented as:
- P(x1,y1)
- Q(x2,y2)
- R(x3,y3)
where x1,y1,x2,y2,x3,y3 are all rational numbers.
2. Find the Centroid of the Triangle:
The centroid (G) of triangle PQR can be calculated using the formula:
G(x1+x2+x33,y1+y2+y33)
Since the sum of rational numbers is rational, both coordinates of the centroid G are rational.
3. Find the Orthocenter of the Triangle:
The orthocenter (H) is the point where the altitudes of the triangle intersect. To find the orthocenter, we need to consider the slopes of the sides and the altitudes:
- The slope of line QR can be calculated as:
mQR=y3−y2x3−x2
- The slope of the altitude from point P to line QR (which is perpendicular to QR) will be:
mPH=−1mQR=−x3−x2y3−y2
The coordinates of the orthocenter can be derived from the equations of the altitudes, which will also yield rational coordinates since they are derived from rational slopes and points.
4. Conclusion:
Since both the centroid and the orthocenter are derived from rational coordinates and operations involving rational numbers, we conclude that:
- The centroid and the orthocenter of triangle PQR are always rational points.
Final Answer:
The points of triangle PQR that are always rational points are:
- The centroid (G)
- The orthocenter (H)
Let the vertices of triangle PQR be represented as:
- P(x1,y1)
- Q(x2,y2)
- R(x3,y3)
where x1,y1,x2,y2,x3,y3 are all rational numbers.
The centroid (G) of triangle PQR can be calculated using the formula:
G(x1+x2+x33,y1+y2+y33)
Since the sum of rational numbers is rational, both coordinates of the centroid G are rational.
The orthocenter (H) is the point where the altitudes of the triangle intersect. To find the orthocenter, we need to consider the slopes of the sides and the altitudes:
- The slope of line QR can be calculated as:
mQR=y3−y2x3−x2
- The slope of the altitude from point P to line QR (which is perpendicular to QR) will be:
mPH=−1mQR=−x3−x2y3−y2
The coordinates of the orthocenter can be derived from the equations of the altitudes, which will also yield rational coordinates since they are derived from rational slopes and points.
Since both the centroid and the orthocenter are derived from rational coordinates and operations involving rational numbers, we conclude that:
- The centroid and the orthocenter of triangle PQR are always rational points.
The points of triangle PQR that are always rational points are:
- The centroid (G)
- The orthocenter (H)
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBook:CENGAGE ENGLISHChapter:COMPLEX NUMBERS AND QUADRATIC EQUATIONSExercise:All Questions
Explore 886 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Book:CENGAGE ENGLISHChapter:DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Exercise:Multiple correct answers type
Explore 11 Videos
Similar Questions
Statement 1: If in a triangle, orthocentre, circumcentre and centroid are rational points, then its vertices must also be rational points.
Statement : 2 If the vertices of a triangle are rational points, then the centroid, circumcentre and orthocentre are also rational points.
View SolutionIf the vertices of a triangle have rational coordinates, then prove that the triangle cannot be equilateral.
View Solution
Knowledge Check
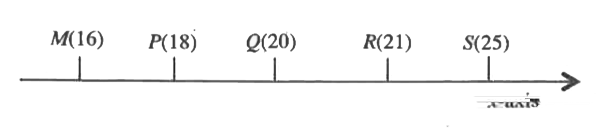
Which one of the following points in the figure is the median of the points M, P, Q, R and S?AMBPCQDR
If the vertices of a triangle have rational coordinates, then prove that the triangle cannot be equilateral.
View SolutionIf the vertices of a triangle have rational coordinates, then prove that the triangle cannot be equilateral.
View SolutionIf the vertices of a triangle have rational coordinates, then prove that the triangle cannot be equilateral.
View SolutionIf the coordinates of vertices of a triangle is always rational then the triangle cannot be
View SolutionA straight line through the vertex P of a triangle PQR intersects the side QR at the points S and the cicumcircle of the triangle PQR at the point T. If S is not the center of the circumcircle, then 1PS+1ST<2√QS×SR 1PS+1ST>2√QS×SR 1PS+1ST<4QR 1PS+1ST>4QR
View SolutionIn the given triangle P, Q and R are the mid points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

View SolutionProve that all the vertices of an equilateral triangle can not be integral points (an integral point is a point both of whose coordinates are integers).
View Solution