A rectangle ABCD, where A≡(0,0),B≡(4,0),C≡(4,2)D≡(0,2) , undergoes the following transformations successively: f1(x,y)−−→y,x f2(x,y)−−−−−−→x+3y,y f3(x,y)−−−−−−−→(x−y)/2,(x+y)/2) The final figure will be square (b) a rhombus a rectangle (d) a parallelogram
To solve the problem, we will apply the transformations step-by-step to the vertices of the rectangle ABCD and determine the final shape.
Step 1: Identify the vertices of the rectangle ABCD.
- A = (0, 0)
- B = (4, 0)
- C = (4, 2)
- D = (0, 2)
Step 2: Apply the first transformation f1(x,y)=(y,x).
This transformation swaps the x and y coordinates of each point.
- A' = f_1(0, 0) = (0, 0)
- B' = f_1(4, 0) = (0, 4)
- C' = f_1(4, 2) = (2, 4)
- D' = f_1(0, 2) = (2, 0)
So, after the first transformation, the new points are:
- A' = (0, 0)
- B' = (0, 4)
- C' = (2, 4)
- D' = (2, 0)
Step 3: Apply the second transformation f2(x,y)=(x+3y,y).
Now we will apply this transformation to the new points.
- A'' = f_2(0, 0) = (0 + 3*0, 0) = (0, 0)
- B'' = f_2(0, 4) = (0 + 3*4, 4) = (12, 4)
- C'' = f_2(2, 4) = (2 + 3*4, 4) = (14, 4)
- D'' = f_2(2, 0) = (2 + 3*0, 0) = (2, 0)
So, after the second transformation, the new points are:
- A'' = (0, 0)
- B'' = (12, 4)
- C'' = (14, 4)
- D'' = (2, 0)
Step 4: Apply the third transformation f3(x,y)=(x−y2,x+y2).
Now we will apply this transformation to the new points.
- A''' = f_3(0, 0) = (0−02,0+02)=(0,0)
- B''' = f_3(12, 4) = (12−42,12+42)=(4,8)
- C''' = f_3(14, 4) = (14−42,14+42)=(5,9)
- D''' = f_3(2, 0) = (2−02,2+02)=(1,1)
So, after the third transformation, the new points are:
- A''' = (0, 0)
- B''' = (4, 8)
- C''' = (5, 9)
- D''' = (1, 1)
Step 5: Determine the shape formed by the new points.
To determine the shape, we can calculate the slopes of the sides formed by the points A''', B''', C''', and D'''.
1. Slope of AB''':
slope=y2−y1x2−x1=8−04−0=2
2. Slope of BC''':
slope=9−85−4=1
3. Slope of CD''':
slope=1−91−5=−8−4=2
4. Slope of DA''':
slope=0−10−1=1
Conclusion:
- The slopes of opposite sides are equal:
- Slope of AB''' = Slope of CD''' = 2
- Slope of BC''' = Slope of DA''' = 1
Since opposite sides are equal in slope, the final figure is a parallelogram.
Final Answer:
The final figure will be a parallelogram.
- A = (0, 0)
- B = (4, 0)
- C = (4, 2)
- D = (0, 2)
This transformation swaps the x and y coordinates of each point.
- B' = f_1(4, 0) = (0, 4)
- C' = f_1(4, 2) = (2, 4)
- D' = f_1(0, 2) = (2, 0)
- A' = (0, 0)
- B' = (0, 4)
- C' = (2, 4)
- D' = (2, 0)
Now we will apply this transformation to the new points.
- B'' = f_2(0, 4) = (0 + 3*4, 4) = (12, 4)
- C'' = f_2(2, 4) = (2 + 3*4, 4) = (14, 4)
- D'' = f_2(2, 0) = (2 + 3*0, 0) = (2, 0)
- A'' = (0, 0)
- B'' = (12, 4)
- C'' = (14, 4)
- D'' = (2, 0)
Now we will apply this transformation to the new points.
- B''' = f_3(12, 4) = (12−42,12+42)=(4,8)
- C''' = f_3(14, 4) = (14−42,14+42)=(5,9)
- D''' = f_3(2, 0) = (2−02,2+02)=(1,1)
- A''' = (0, 0)
- B''' = (4, 8)
- C''' = (5, 9)
- D''' = (1, 1)
To determine the shape, we can calculate the slopes of the sides formed by the points A''', B''', C''', and D'''.
slope=y2−y1x2−x1=8−04−0=2
slope=9−85−4=1
slope=1−91−5=−8−4=2
slope=0−10−1=1
- The slopes of opposite sides are equal:
- Slope of AB''' = Slope of CD''' = 2
- Slope of BC''' = Slope of DA''' = 1
The final figure will be a parallelogram.
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBook:CENGAGE ENGLISHChapter:COMPLEX NUMBERS AND QUADRATIC EQUATIONSExercise:All Questions
Explore 886 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Book:CENGAGE ENGLISHChapter:DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Exercise:Multiple correct answers type
Explore 11 Videos
Similar Questions
If the square ABCD, where A(0,0),B(2,0)C(2,2)andD(0,2) undergoes the following three transformations successively
(i) f1(x,y)→(y,x)
(ii) f2(x,y)→(x+3y,y)
(iii) f3(x,y)→(x−y2,x+y2)
then the final figure is a
View SolutionFor what values of x and y are the following matrices equal? A=[2x+12y0y2−5y] , B=[x+3y2+20−6]
View SolutionThe following line(s) is (are) tangent to the curve y=x2−x (A) x−y=0 (B) x+y=0 (C) x−y=1 (D) x+y=1
View SolutionThe figure formed by the lines ax±y±c=0 is a. a rectangle b. a square c. a rhombus d. none of these
View SolutionExamples :- If x;y∈{1;2;3;4};then which of the following are function in the given set ? (a) f_1={(x;y):y=(x+1)} (b) f_2={(x;y):y4 (d) f_4={(x;y):x+y=5}
View SolutionThe equation of the incircle of equilateral triangle ABC where B≡(2,0),C≡(4,0), and A lies in the fourth quadrant is: (a) x2+y2−6x+2y√3+9=0 (b) x2+y2−6x−2y√3+9=0 (c) x2+y2+6x+2y√3+9=0 (d) none of these
View SolutionGiven the graph of y=f(x).
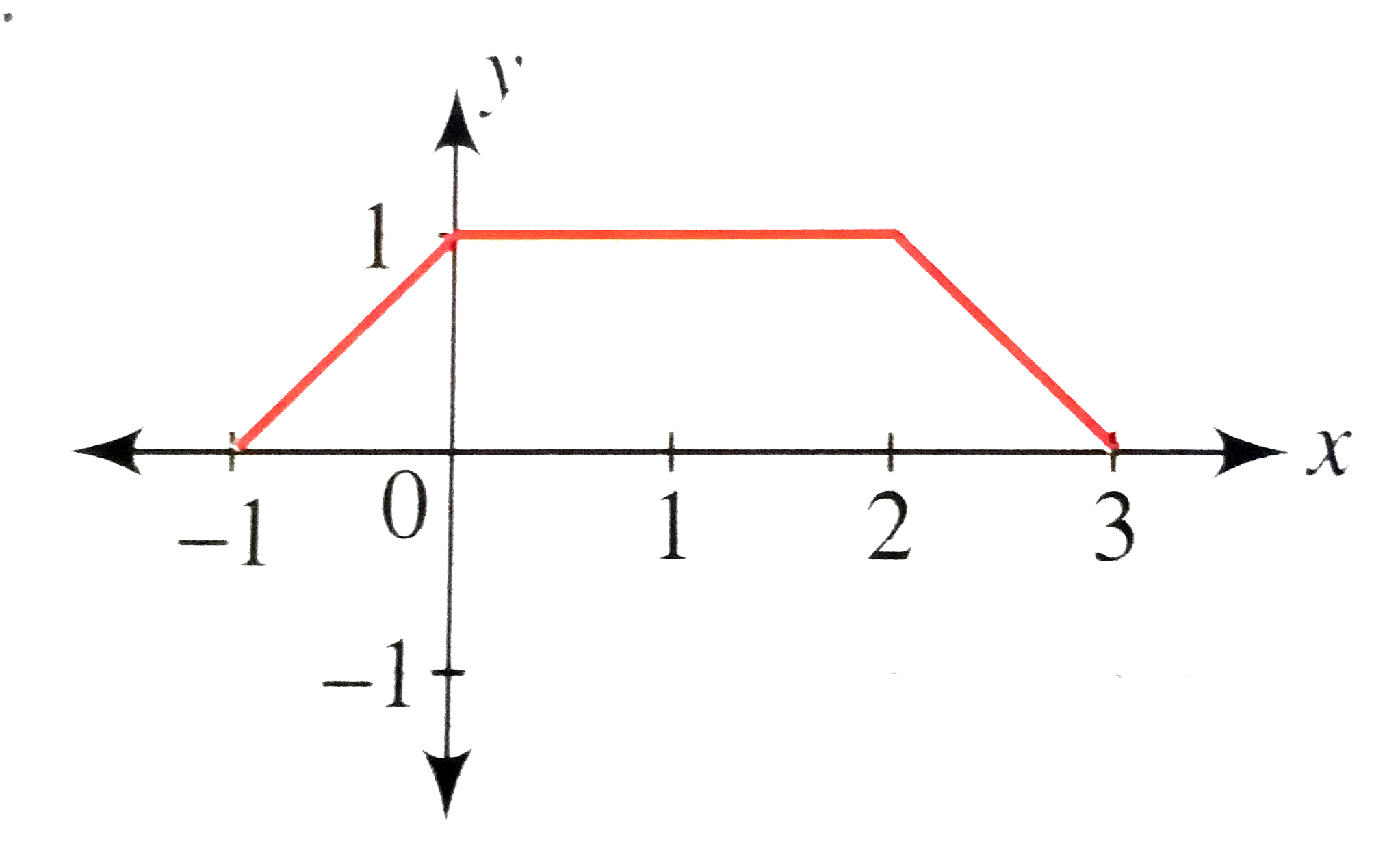
Draw the graphs of the followin.
(a) y=f(1−x) (b) y=−2f(x)
(c) y=f(2x) (d) y=1−f(x)
View SolutionIf a function satisfies (x-y)f(x+y)-(x+y)f(x-y)=2(x^2 y-y^3) AA x, y in R and f(1)=2, then a) f(x) must be polynomial function, b) f(3)=12, c) f(0)=0, d) f(x) may not be differentiable.
View SolutionLet f(x) be defined for all x>0 and be continuous. Let f(x) satisfies f(xy)=f(x)−f(y) for all x,yandf(e)=1. Then (a) f(x) is unbounded (b) f(1x)→0 as x→0 (c) f(x) is bounded (d) f(x)=(log)ex
View SolutionThe factors of x3−x2y−xy2+y3 are
(a(x+y)(x2−xy+y2)
(b) (x+y)(x2+xy+y2)
(c)(x+y)2(x−y)
(d) (x−y)2(x+y)
View Solution