A line is a drawn from P(4,3) to meet the lines L1andl2 given by 3x+4y+5=0and3x+4y+15=0 at points AandB respectively. From A , a line perpendicular to L is drawn meeting the line L2 at A1 Similarly, from point B1 Thus a parallelogram ∀1BB1 is formed. Then the equation of L so that the area of the parallelogram ∀1BB1 is the least is (a) x−7y+17=0 (b) 7x+y+31=0 (c) x−7y−17=0 (d) x+7y−31=0
Step by step video & image solution for A line is a drawn from P(4,3) to meet the lines L_1 and l_2 given by 3x+4y+5=0 and 3x+4y+15=0 at points A and B respectively. From A , a line perpendicular to L is drawn meeting the line L_2 at A_1 Similarly, from point B_1 Thus a parallelogram AA_1 B B_1 is formed. Then the equation of L so that the area of the parallelogram AA_1 B B_1 is the least is (a) x-7y+17=0 (b) 7x+y+31=0 (c) x-7y-17=0 (d) x+7y-31=0 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A line L passing through (1, 1) intersect lines L1:12x+5y=13 and L2:12x+5y=65 at A and B respectively. If AB=5 , then line L can be
View SolutionA variable line L is drawn through O(0,0) to meet the line L1 and L2 given by y-x-10 =0 and y-x-20=0 at Points A and B, respectively.
Locus of P, if OP2=OA×OB, is a. (y+x)2=50 b. (y−x)2=200 c. (y−x)2=100 d. none of these
View SolutionA variable line L drawn through O(0,0) to meet line l1: y-x-10=0 and L2:y-x-20=0 at the point A and B respectively then locus of point p is ' such that (OP)2=OA.OB,
View SolutionA variable line L is drawn through O (0,0) to meet the lines L 1 :y−x−10=0 and L 2 :y−x−20=0 at the points A and B respectively. A point P is taken on L such that OP 2 = OA 1 + OB 1 and P,A,B lies on same side of origin O. The locus of P is
View SolutionFind the length of perpendicular drawn from point (2,−1) to the line 3x+4y−11=0.
View SolutionThe line y=3x4 meets the lines x−y+1=0 and 2x−y=5 at A and B respectively. Coordinates of P on y=3x4 such that PA⋅PB=25.
View SolutionGiven equation of line L1 is y=4
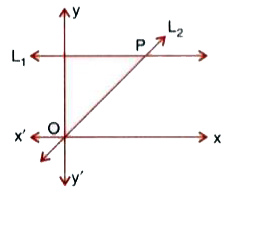
Write the slope of line L1 if L2 is the bisector of angle O.
View SolutionA line intersects the straight lines 5x−y−4=0 and 3x−4y−4=0 at A and B , respectively. If a point P(1,5) on the line AB is such that AP:PB=2:1 (internally), find point A.
View SolutionA straight line L is perpendicular to the line 5x−y=1. The area of the triangle formed by the line L and the coordinate axes is 5'□units.F∈dtheequationofthel∈eL
View SolutionFind the distance of the point P from the line l in that : l:xa−yb=1andP≡(b,a)
View Solution
