Triangle ABC with AB=13,BC=5, and AC=12 slides on the coordinates axes with AandB on the positive x-axis and positive y-axis respectively. The locus of vertex C is a line 12x−ky=0. Then the value of k is_____________
To solve the problem, we need to find the value of k in the equation of the line 12x−ky=0 that represents the locus of vertex C of triangle ABC as it slides along the coordinate axes.
1. Identify the Triangle Configuration:
We have triangle ABC with sides AB=13, BC=5, and AC=12. Since 122+52=132 (i.e., 144+25=169), triangle ABC is a right triangle with the right angle at vertex C.
Hint: Use the Pythagorean theorem to confirm the right angle in triangle configurations.
2. Position the Triangle:
Place point A at (0,0) on the coordinate plane, point B on the positive x-axis at (xA,0), and point C on the positive y-axis at (0,yB). Thus, the coordinates of points are:
- A(0,0)
- B(xA,0)
- C(0,yB)
3. Use the Lengths to Set Up Equations:
The lengths of the sides give us the following equations:
- AB=13: √x2A+y2B=13
- AC=12: yB=12
- BC=5: √(xA−0)2+(0−12)2=5
4. Substituting for yB:
From AC=12, we have yB=12. Now substituting yB into the equation for BC:
√x2A+122=5
Squaring both sides:
x2A+144=25
Rearranging gives:
x2A=25−144=−119
This indicates that BC cannot be 5 when AC=12 and AB=13 since the triangle inequality must hold.
5. Finding the Locus of C:
Since C is at (0,yB) and yB is fixed at 12, we can express the relationship between xA and yB using the tangent of the angle at C:
tan(θ)=BCAC=512
This gives us the slope of the line representing the locus of C.
6. Setting Up the Equation:
The slope of the line from A to C can be expressed as:
yBxA=512
Rearranging gives:
12yB=5xA
or equivalently:
12x−ky=0
where k=5.
7. Conclusion:
Therefore, the value of k is 5.
Final Answer:
The value of k is 5.
We have triangle ABC with sides AB=13, BC=5, and AC=12. Since 122+52=132 (i.e., 144+25=169), triangle ABC is a right triangle with the right angle at vertex C.
Place point A at (0,0) on the coordinate plane, point B on the positive x-axis at (xA,0), and point C on the positive y-axis at (0,yB). Thus, the coordinates of points are:
- A(0,0)
- B(xA,0)
- C(0,yB)
The lengths of the sides give us the following equations:
- AB=13: √x2A+y2B=13
- AC=12: yB=12
- BC=5: √(xA−0)2+(0−12)2=5
From AC=12, we have yB=12. Now substituting yB into the equation for BC:
√x2A+122=5
Squaring both sides:
x2A+144=25
Rearranging gives:
x2A=25−144=−119
This indicates that BC cannot be 5 when AC=12 and AB=13 since the triangle inequality must hold.
Since C is at (0,yB) and yB is fixed at 12, we can express the relationship between xA and yB using the tangent of the angle at C:
tan(θ)=BCAC=512
This gives us the slope of the line representing the locus of C.
The slope of the line from A to C can be expressed as:
yBxA=512
Rearranging gives:
12yB=5xA
or equivalently:
12x−ky=0
where k=5.
Therefore, the value of k is 5.
The value of k is 5.
Topper's Solved these Questions
Similar Questions
An isosceles right traingle ABC with BC = AC slides on the axes with A and B on x and y axes respectively. The locus of C is …………… .
View SolutionA right angled triangle ABC having a right angle at C, CA=b and CB=a, move such that angular points A and B slide along x-axis and y-axis respectively. Find the locus of C
View Solution
Knowledge Check
If a, b, c are the angles that a line makes with the positive directions of x, y and z axis, respectively, then the direction cosines of the lines are
Asin a, sin b, sin cBcos a, cos b, cos cCtan a, tan b, tan cDnone of the aboveΔABC , shown below in the standard (x,y) coordinate plane is equilateral with vertex A at (0,w) and vertex B on the x- axis as shown . What are the coordinates of vertex C ?
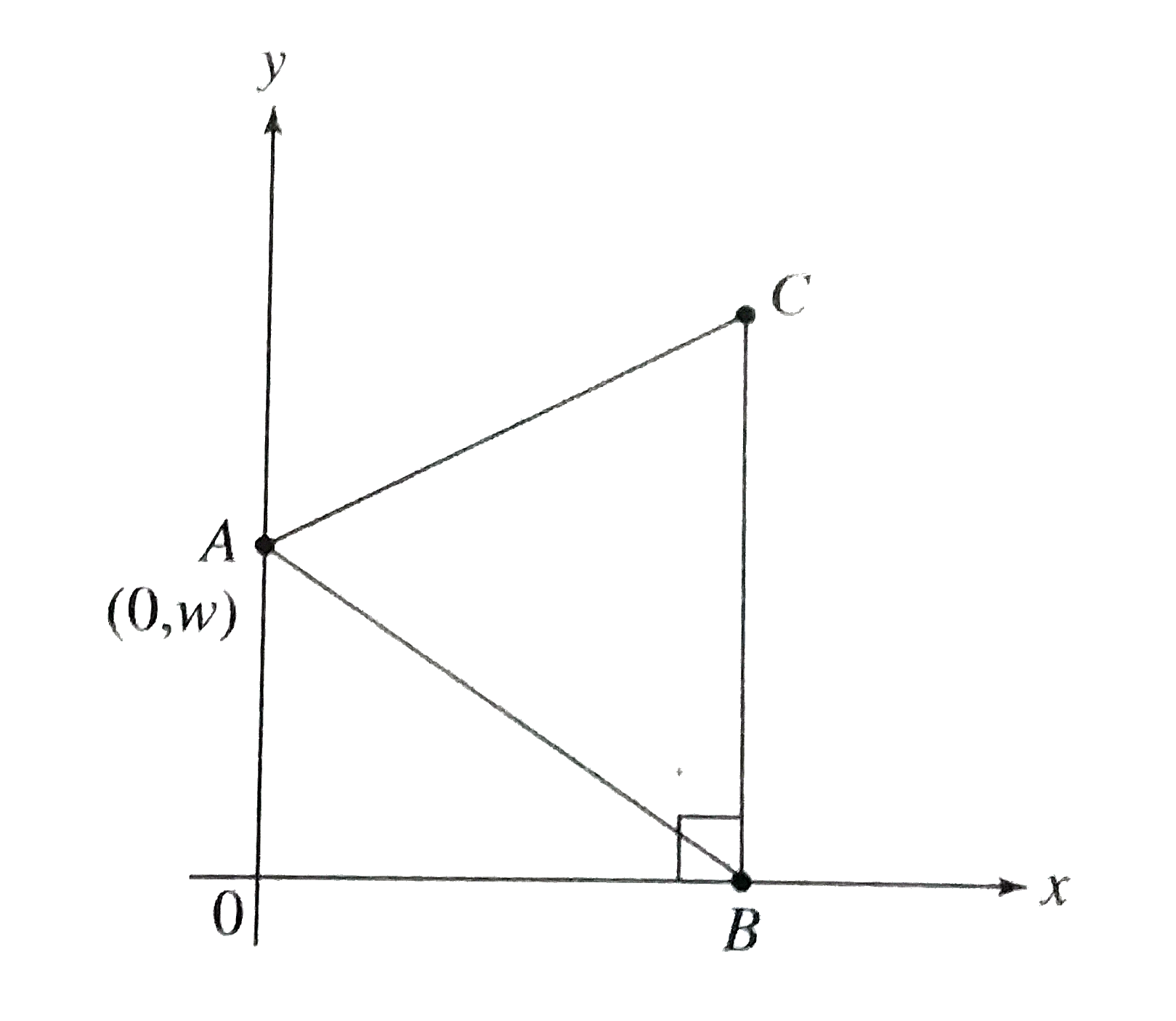 A(w,0)B(w,2w)C(w√3,w)D(w√3,2w)
A(w,0)B(w,2w)C(w√3,w)D(w√3,2w)
Suppose a parabola y=x2−ax−1 intersects the coordinate axes at three points A,B and C, respectively. The circumcircle of ΔABC intersects the y-axis again at the point D(0,t). Then the value of t is
View SolutionA rectangle ABCD has its side AB parallel to line y=x, and vertices A,BandD lie on y=1,x=2, and x=−2, respectively. The locus of vertex C is x=5 (b) x−y=5 y=5 (d) x+y=5
View SolutionABCD is square in which A lies on positive y-axis and B lies on the positive x-axis. If D is the point (12, 17), then co-ordinate of C is
View SolutionABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(−2,7) , the coordinates of vertex A
View SolutionIf on a given base BC[B(0,0) and C(2,0)], a triangle is described such that the sum of the base angles is 4, then the equation of the locus of the opposite vertex A is parabola whose directrix is y=k. The value of k is _________ .
View SolutionThe foot of the perpendicular on the line 3x+y=λ drawn from the origin is C. If the line cuts the x and the y-axis at AandB , respectively, then BC:CA is
View Solution
