Question

Given A(0,0) and B(x,y) with x$\in$(0,1) and y>0. Let the slope of line AB be $m_1$. Point C lies on line $x=1$ such that the slope of BC is equal to $m_2$ where$0<m_2<m_1$. If the area of triangle ABC can be expressed as $(m_1-m_2)f\left(x\right)$ then the largest possible value of x is

Options

A. 1
B. `1//2`
C. `1//4`
D. `1//8`

Explanation

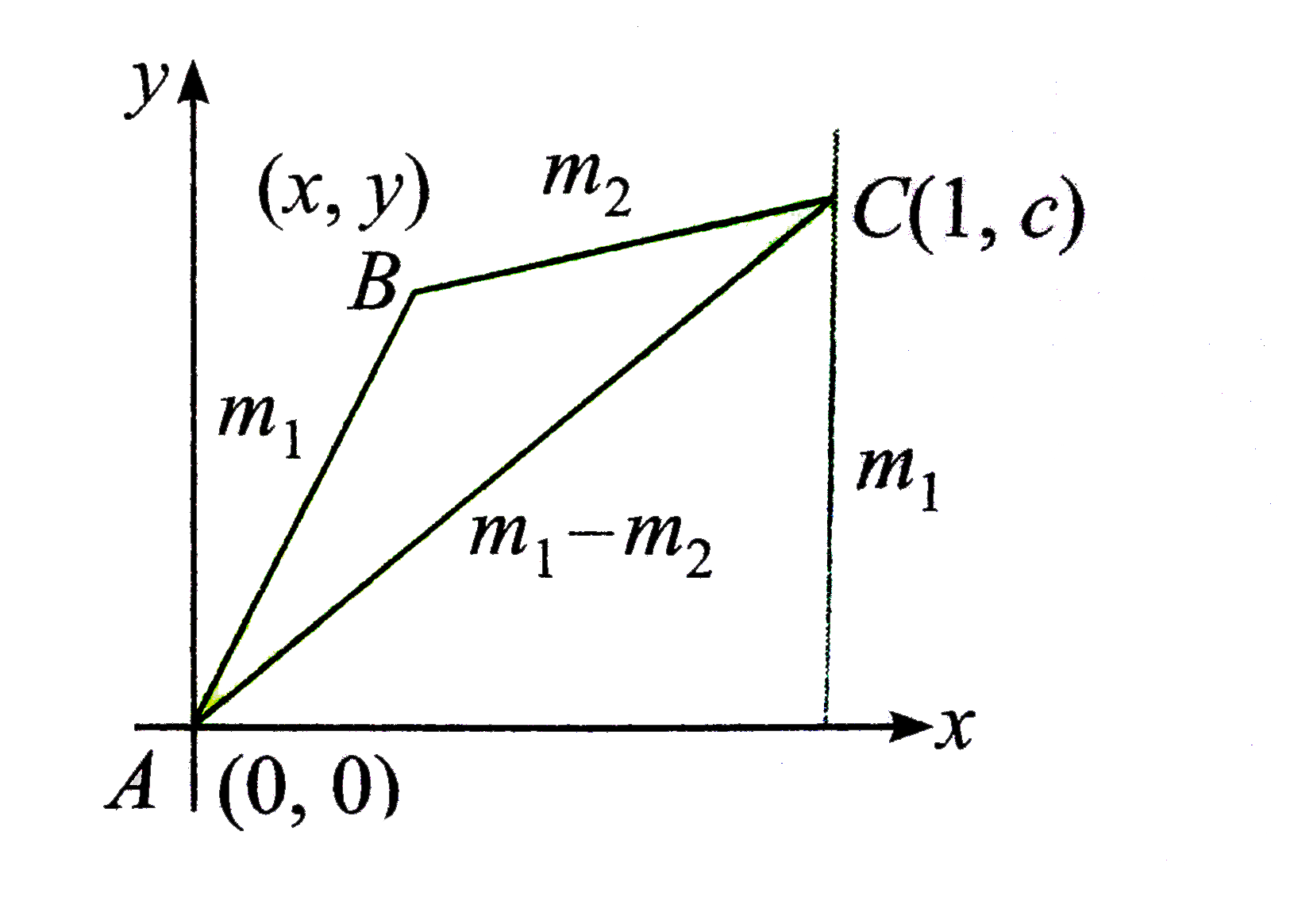
Let the coordinates of C be (1,c). Then,
`m_(2) = (c-y)/(1-x)`
`"or " m_(2) = (c-m_(1)x)/(1-x)`
`"or " m_(2)-m_(2)x = c-m_(1)x`
`"or " (m_(1)-m_(2))x = c-m_(2)`
`"or " c = (m_(1)-m_(2))x + m_(2) " " (1)`
Now, the area of `DeltaABC` is
`(1)/(2)||{:(0,0,1),(x,m_(1)x,1),(1,c,1):}|| = (1)/(2) |[cx-m_(1)x]|`
`=(1)/(2)|[{(m_(1)-m_(2))x+m_(2)}x-m_(1)x]|`
`=(1)/(2)|[(m_(1)-m_(2))x^(2)+m_(2)x-m_(1)x]|`
`=(1)/(2)(m_(1)-m_(2))(x-x^(2)) " " [because x gt x^(2) "in" (0,1)]`
`"Hence, " f(x) = (1)/(2)(x-x^(2))`
`f(x)_(max) = (1)/(8) "when " x =(1)/(2)`