A straight line L through the point (3,-2) is inclined at an angle $60^{\circ}$ to the line $\sqrt{3} x + y = 1$ . If L also intersects the x-axis then find the equation of L .

$y + \sqrt{3} x + 2 - 3 \sqrt{3} = 0$

$y - \sqrt{3} x + 2 + 3 \sqrt{3} = 0$

$\sqrt{3} y - x + 3 + 2 \sqrt{3} = 0$

$\sqrt{3} y + x - 3 + 2 \sqrt{3} = 0$

Video Solution

Text Solution

Verified by Experts

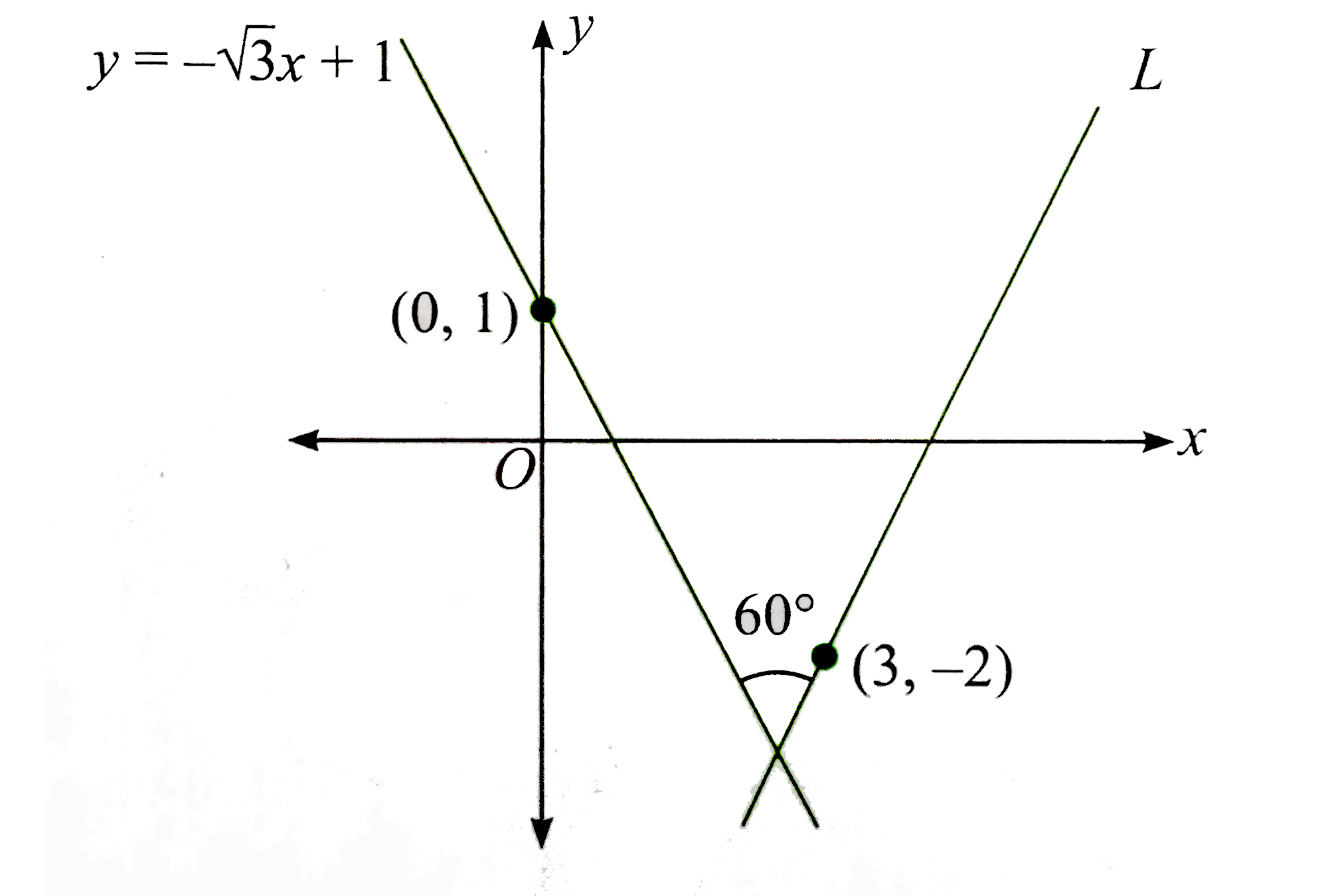
Let the slope of the required line be m. Then
$∣ ∣ ∣ \frac{m + \sqrt{3}}{1 - \sqrt{3} m} ∣ ∣ ∣ = \sqrt{3}$
$∴ m + \sqrt{3} = \pm (\sqrt{3} - 3 m)$
$∴ m = 0 or m = \sqrt{3}$
Therefore, the equation is
$y + 2 = \sqrt{3} (x - 3) (m \neq 0 as given that line cuts the x-axis)$
$or \sqrt{3} x - y - (2 + 3 \sqrt{3}) = 0$

Updated on:21/07/2023