In a trapezium, the vector BC=λAD. We will then find that p=AC+BD is collinear with AD. I p=μ AD, then
Step by step video & image solution for In a trapezium, the vector BC=lamdaAD. We will then find that p=AC+BD is collinear with AD. I p=mu AD, then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS EXERCISE - Multiple Correct Answers Type
6 Videos
- VECTORS TRIPLE PRODUCTS, RECIPROCAL SYSTEM OF VECTORSBOOK - CENGAGE ENGLISHCHAPTER - VECTORS TRIPLE PRODUCTS, RECIPROCAL SYSTEM OF VECTORSEXERCISE - DPP 2.4
20 Videos
Similar Questions
In a trapezium ABCD the vector B→C=λ−−→AD. If →p=A→C+−−→BD is coillinear with −−→AD such that →p=μ−−→AD, then
View SolutionIn a trapezium ABCD the vector B→C=α−−→AD. If →p=A→C+−−→BD is coillinear with −−→AD such that →p=μ−−→AD, then
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
ΔAPB is similar to ΔCPD.
View SolutionThe given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3:5,
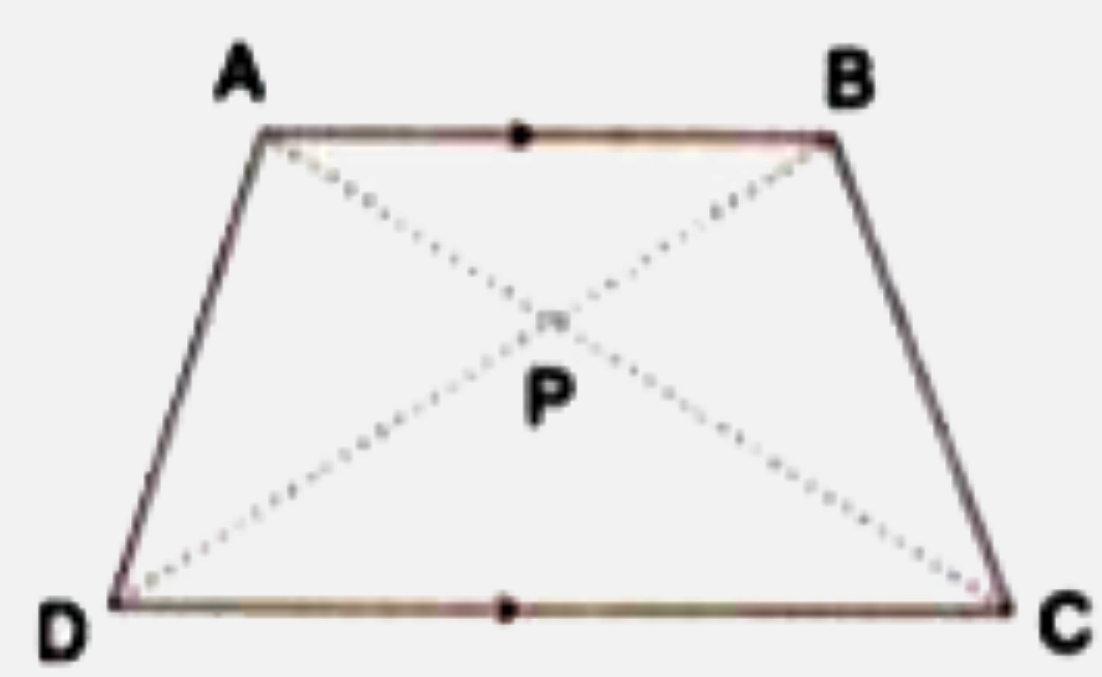
Find :
ΔAPB:ΔADB
View SolutionThe given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3:5,

Find :
ΔADP:ΔAPB
View SolutionThe given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3:5,

Find :
ΔDPC:ΔAPB
View SolutionThe given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3:5,

Find :
ΔAPB:ΔCPB
View SolutionIn the adjoining figure, O is the centre of a circle in which AB and CD are two diameters. Prove that AC| |BD and AD| |BC. If ∠OBD=50∘, then find the value of ∠AOC.

View SolutionIn figure, DE||BC and the ratio of the areas of △ADEand trapezium BDEC is 4:5 . Find the ratio of DE:BC . If BD = 2cm. Then find AD.
View SolutionIn trapezium ABCD, side AB is parallel to side DC. Diagonals AC and BD intersect at point P. Prove that triangles APD and BPC are equal in area.
View Solution
