n
whole are randomly chosen and multiplied
Column I,
Column II
The
probability that the last digit is 1,3,7, or 9 is, p. 8n−4n10n
The
probability that the last digit is 2,4,6, or 8 is, q. 5n−4n10n
The
probability that the last digit is 5 is, r. 4n10n
The
probability that the last digit is zero is, s. 10n−8n−5n+4n10n
To solve the problem, we need to find the probabilities of the last digit of the product of n randomly chosen whole numbers. We will analyze each case step by step.
Step 1: Probability that the last digit is 1, 3, 7, or 9 (p)
The last digit of a number can be one of 0, 1, 2, 3, 4, 5, 6, 7, 8, or 9. The digits 1, 3, 7, and 9 are odd and not divisible by 2 or 5.
- There are 4 favorable outcomes (1, 3, 7, 9) out of 10 possible outcomes (0-9).
- The probability that the last digit of the product is one of these is given by:
\(
p = \left(\frac{4}{10}\right)^n = \frac{4^n}{10^n}
\)
However, we need to consider that we want the last digit to be 1, 3, 7, or 9 in all n numbers chosen. Therefore, the total number of ways to choose numbers such that the last digit is one of these four is \(8^n\) (since we can choose from 0-9 but avoid 2, 4, 5, 6, 8). Thus:
\(
p = \frac{8^n - 4^n}{10^n}
\)
Step 2: Probability that the last digit is 2, 4, 6, or 8 (q)
The last digit can be 2, 4, 6, or 8, which are the even digits.
- There are 4 favorable outcomes (2, 4, 6, 8) out of 10 possible outcomes.
- The probability that the last digit of the product is one of these is given by:
\(
q = \left(\frac{4}{10}\right)^n = \frac{4^n}{10^n}
\)
However, we can also find this by considering the total outcomes:
\(
q = \frac{5^n - 4^n}{10^n}
\)
Step 3: Probability that the last digit is 5 (r)
The last digit can be 5.
- There is only 1 favorable outcome (5) out of 10 possible outcomes.
- The probability that the last digit of the product is 5 is given by:
\(
r = \left(\frac{1}{10}\right)^n = \frac{1^n}{10^n}
\)
However, we can also find this by considering the total outcomes:
\(
r = \frac{4^n}{10^n}
\)
Step 4: Probability that the last digit is 0 (s)
The last digit can be 0.
- There is only 1 favorable outcome (0) out of 10 possible outcomes.
- The probability that the last digit of the product is 0 is given by:
\(
s = \left(\frac{1}{10}\right)^n = \frac{1^n}{10^n}
\)
However, we can also find this by considering the total outcomes:
\(
s = \frac{10^n - 8^n - 5^n + 4^n}{10^n}
\)
Summary of Results
- The probability that the last digit is 1, 3, 7, or 9 is \( p = \frac{8^n - 4^n}{10^n} \)
- The probability that the last digit is 2, 4, 6, or 8 is \( q = \frac{5^n - 4^n}{10^n} \)
- The probability that the last digit is 5 is \( r = \frac{4^n}{10^n} \)
- The probability that the last digit is 0 is \( s = \frac{10^n - 8^n - 5^n + 4^n}{10^n} \)
The last digit of a number can be one of 0, 1, 2, 3, 4, 5, 6, 7, 8, or 9. The digits 1, 3, 7, and 9 are odd and not divisible by 2 or 5.
- The probability that the last digit of the product is one of these is given by:
\(
p = \left(\frac{4}{10}\right)^n = \frac{4^n}{10^n}
\)
\(
p = \frac{8^n - 4^n}{10^n}
\)
The last digit can be 2, 4, 6, or 8, which are the even digits.
- The probability that the last digit of the product is one of these is given by:
\(
q = \left(\frac{4}{10}\right)^n = \frac{4^n}{10^n}
\)
\(
q = \frac{5^n - 4^n}{10^n}
\)
The last digit can be 5.
- The probability that the last digit of the product is 5 is given by:
\(
r = \left(\frac{1}{10}\right)^n = \frac{1^n}{10^n}
\)
\(
r = \frac{4^n}{10^n}
\)
The last digit can be 0.
- The probability that the last digit of the product is 0 is given by:
\(
s = \left(\frac{1}{10}\right)^n = \frac{1^n}{10^n}
\)
\(
s = \frac{10^n - 8^n - 5^n + 4^n}{10^n}
\)
- The probability that the last digit is 1, 3, 7, or 9 is \( p = \frac{8^n - 4^n}{10^n} \)
- The probability that the last digit is 2, 4, 6, or 8 is \( q = \frac{5^n - 4^n}{10^n} \)
- The probability that the last digit is 5 is \( r = \frac{4^n}{10^n} \)
- The probability that the last digit is 0 is \( s = \frac{10^n - 8^n - 5^n + 4^n}{10^n} \)
Similar Questions
Knowledge Check
Match Column I with Column II.
 AA - p, B - q, C - r, D - sBA - r, B - s, C - p, D - qCA - s, B - p, C- q, D - rDA - q, B - r, C - s, D - p
AA - p, B - q, C - r, D - sBA - r, B - s, C - p, D - qCA - s, B - p, C- q, D - rDA - q, B - r, C - s, D - pMatch the Column I and Column II:
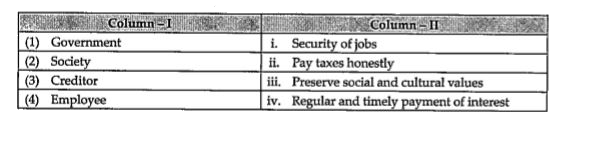 A1. i. 2. ii 3. iii 4. ivB1. i 2. ii 3. iii 4. ivC1. i2. ii 3. iii 4. ivD1. i 2. ii 3. iii 4. iv
A1. i. 2. ii 3. iii 4. ivB1. i 2. ii 3. iii 4. ivC1. i2. ii 3. iii 4. ivD1. i 2. ii 3. iii 4. ivMatch the Column I and Column II:
 A1. i 2. ii 3. iii 4. ivB1. i 2. ii 3. iii 4. ivC1. i 2. ii 3. iii 4. ivD1. i 2. ii 3. iii 4. iv
A1. i 2. ii 3. iii 4. ivB1. i 2. ii 3. iii 4. ivC1. i 2. ii 3. iii 4. ivD1. i 2. ii 3. iii 4. iv
Match Column I with Column II.

View SolutionMatch Column I with Column II.

View SolutionTwo whole numbers are randomly chosen and multiplied, then the chance that their product is divisible by 5 is
View SolutionMatch the column-I and Column II-

View SolutionMatch Column I with Column II
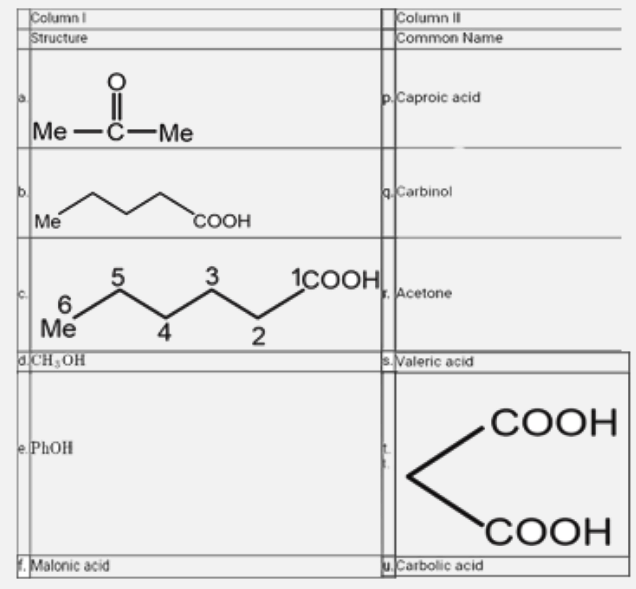
View Solution


