A circle of radius unity is centered at thet origin. Two particles tart moving at the same time from the point (1,0) and move around the circle in opposite direction. One of the particle moves anticlockwise with constant speed v and the other moves clockwise with constant speed 3v. After leaving (1,0), the two particles meet first at a point P, and continue until they meet next at point Q. The coordinates of the point Q are
To solve the problem, we need to determine the coordinates of the point Q where the two particles meet after starting from the point (1,0) on a unit circle.
1. Understanding the Motion of the Particles:
- Particle A moves anticlockwise with speed v.
- Particle B moves clockwise with speed 3v.
- They start from the point (1,0).
2. Finding the Time of First Meeting:
- The distance covered by both particles when they meet for the first time is equal to the circumference of the circle.
- The circumference C of the circle is given by C=2πr where r=1. Thus, C=2π.
3. Setting Up the Equation:
- Let t be the time taken until they meet.
- Distance covered by Particle A in time t is vt (anticlockwise).
- Distance covered by Particle B in time t is 3vt (clockwise).
- Since they are moving in opposite directions, the total distance covered when they meet is:
vt+3vt=2π
- This simplifies to:
4vt=2π
4. Solving for Time t:
- Rearranging gives:
t=2π4v=π2v
5. Finding the Position of Each Particle at Time t:
- The angle covered by Particle A (anticlockwise) in time t is:
θA=vt1=v⋅π2v=π2
- The angle covered by Particle B (clockwise) in time t is:
θB=3v⋅t=3v⋅π2v=3π2
6. Finding Coordinates of Point P:
- The coordinates of Particle A after time t (at angle π2) are:
P=(cos(π2),sin(π2))=(0,1)
7. Finding the Time Until They Meet Again:
- After meeting at P, they continue moving.
- The next meeting point Q occurs when the total distance traveled again equals the circumference 2π.
- The time taken to meet again can be calculated similarly:
4vt′=2π⇒t′=π2v
- The total time from the start to the second meeting is:
t+t′=π2v+π2v=πv
8. Finding the Position of Each Particle at Time t+t′:
- For Particle A:
θA=v⋅πv=π
- For Particle B:
θB=3v⋅πv=3π
9. Finding Coordinates of Point Q:
- The coordinates of Particle A after time πv (at angle π) are:
Q=(cos(π),sin(π))=(−1,0)
Final Answer:
The coordinates of the point Q are (−1,0).
- Particle A moves anticlockwise with speed v.
- Particle B moves clockwise with speed 3v.
- They start from the point (1,0).
- The distance covered by both particles when they meet for the first time is equal to the circumference of the circle.
- The circumference C of the circle is given by C=2πr where r=1. Thus, C=2π.
- Let t be the time taken until they meet.
- Distance covered by Particle A in time t is vt (anticlockwise).
- Distance covered by Particle B in time t is 3vt (clockwise).
- Since they are moving in opposite directions, the total distance covered when they meet is:
vt+3vt=2π
- This simplifies to:
4vt=2π
- Rearranging gives:
t=2π4v=π2v
- The angle covered by Particle A (anticlockwise) in time t is:
θA=vt1=v⋅π2v=π2
- The angle covered by Particle B (clockwise) in time t is:
θB=3v⋅t=3v⋅π2v=3π2
- The coordinates of Particle A after time t (at angle π2) are:
P=(cos(π2),sin(π2))=(0,1)
- After meeting at P, they continue moving.
- The next meeting point Q occurs when the total distance traveled again equals the circumference 2π.
- The time taken to meet again can be calculated similarly:
4vt′=2π⇒t′=π2v
- The total time from the start to the second meeting is:
t+t′=π2v+π2v=πv
- For Particle A:
θA=v⋅πv=π
- For Particle B:
θB=3v⋅πv=3π
- The coordinates of Particle A after time πv (at angle π) are:
Q=(cos(π),sin(π))=(−1,0)
The coordinates of the point Q are (−1,0).
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions
886 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
Knowledge Check
A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
 AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
Two particles executing SHM of same frequency, meet at x=+A/2, while moving in opposite direction . Phase difference between the particles is
View SolutionA particle moves in a circle of radius 5 cm with constant speed and time period 0.2πs. The acceleration of the particle is
View SolutionTwo particles of equal mass are moving along the same straight line with the same speed in opposite direction. What is the speed of the centre of mass of the system ?
View SolutionTwo particles of equal mass are moving along the same straight line with the same speed in opposite direction. What is the speed of the centre of mass of the system ?
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
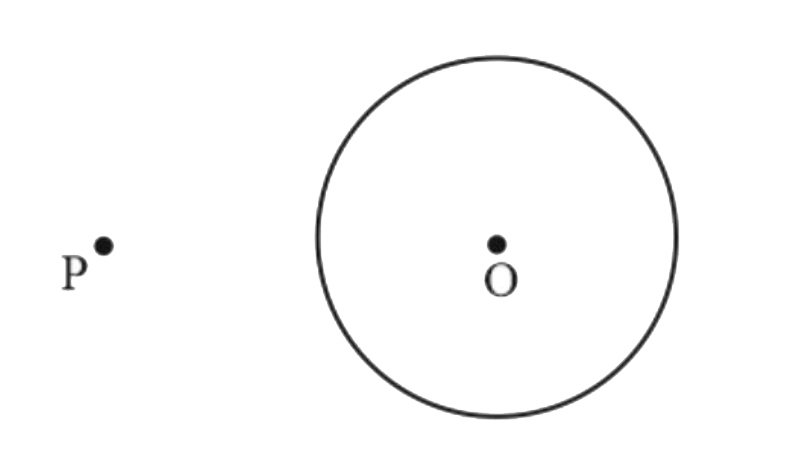
View SolutionConsider a particle , moving in a circle with constant speed . P is a point outside the circle , in the same plane . Then , the angular momentum of the particle about the point P is
View SolutionA particle moving in uniform circle makes 18 revolutions in 1 minutes. If the radius of the circle is 10 cm, the speed of the particle is
View Solution