As shown in the figure, three circles which have the same radius r,have centres at (0,0);(1,1)and(2,1). If they have a common tangentline, as shown then, their radius 'r' is -
To solve the problem, we need to find the radius r of three circles centered at (0,0), (1,1), and (2,1) that have a common tangent line. Here’s a step-by-step solution:
Step 1: Understand the Geometry
We have three circles:
- Circle 1: Center at (0,0) with radius r
- Circle 2: Center at (1,1) with radius r
- Circle 3: Center at (2,1) with radius r
The common tangent line touches all three circles at some point above the x-axis.
Step 2: Set Up the Equation of the Tangent Line
Let the equation of the tangent line be:
y=mx+c
where m is the slope and c is the y-intercept.
Step 3: Calculate the Distance from the Centers to the Tangent Line
The distance d from a point (x0,y0) to the line Ax+By+C=0 is given by:
d=|Ax0+By0+C|√A2+B2
For our line y=mx+c, we can rewrite it as:
mx−y+c=0
Here, A=m, B=−1, and C=c.
Distance from Circle 1 (0,0):
d1=|m(0)−1(0)+c|√m2+1=|c|√m2+1=r
Distance from Circle 2 (1,1):
d2=|m(1)−1(1)+c|√m2+1=|m+c−1|√m2+1=r
Distance from Circle 3 (2,1):
d3=|m(2)−1(1)+c|√m2+1=|2m+c−1|√m2+1=r
Step 4: Set Up the Equations
From the distances, we have:
1. |c|√m2+1=r (1)
2. |m+c−1|√m2+1=r (2)
3. |2m+c−1|√m2+1=r (3)
Step 5: Equate the Distances
From equations (1), (2), and (3), we can equate the expressions for r:
|c|=|m+c−1|(4)
|c|=|2m+c−1|(5)
Step 6: Solve the Equations
Let’s solve equation (4):
- Case 1: c=m+c−1 → m=1
- Case 2: c=−m−c+1 → 2c=1−m → c=1−m2
Now, substitute c from Case 2 into equation (5):
|c|=|2m+1−m2−1|
We can solve for m and then find c.
Step 7: Find the Radius r
Once we have m and c, we can substitute back into equation (1) to find r:
r=|c|√m2+1
Final Calculation
After substituting the values, we will arrive at the final value of r.
We have three circles:
- Circle 1: Center at (0,0) with radius r
- Circle 2: Center at (1,1) with radius r
- Circle 3: Center at (2,1) with radius r
Let the equation of the tangent line be:
y=mx+c
where m is the slope and c is the y-intercept.
The distance d from a point (x0,y0) to the line Ax+By+C=0 is given by:
d=|Ax0+By0+C|√A2+B2
For our line y=mx+c, we can rewrite it as:
mx−y+c=0
Here, A=m, B=−1, and C=c.
d1=|m(0)−1(0)+c|√m2+1=|c|√m2+1=r
d2=|m(1)−1(1)+c|√m2+1=|m+c−1|√m2+1=r
d3=|m(2)−1(1)+c|√m2+1=|2m+c−1|√m2+1=r
From the distances, we have:
1. |c|√m2+1=r (1)
2. |m+c−1|√m2+1=r (2)
3. |2m+c−1|√m2+1=r (3)
From equations (1), (2), and (3), we can equate the expressions for r:
|c|=|m+c−1|(4)
|c|=|2m+c−1|(5)
Let’s solve equation (4):
- Case 1: c=m+c−1 → m=1
- Case 2: c=−m−c+1 → 2c=1−m → c=1−m2
|c|=|2m+1−m2−1|
We can solve for m and then find c.
Once we have m and c, we can substitute back into equation (1) to find r:
r=|c|√m2+1
After substituting the values, we will arrive at the final value of r.
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions
886 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
Knowledge Check
In the shown in the given figure, the resistances R1andR2 are respectively
 A14Ωand40ΩB40Ωand44ΩC40Ωand30ΩD14Ωand30Ω
A14Ωand40ΩB40Ωand44ΩC40Ωand30ΩD14Ωand30Ω
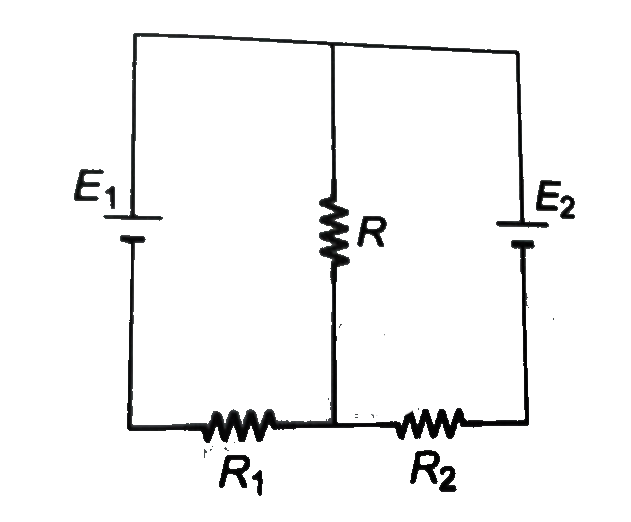
In the circuit shown in figure, the emfs of batteries are E1, and E2 which have internal resistances R1, and R2. At what value of the resistance R will the thermal power generated in it be the highest? What it is?
View SolutionIn the figure, when the outer circles all have radii 'r', then the radius of the inner circle will be
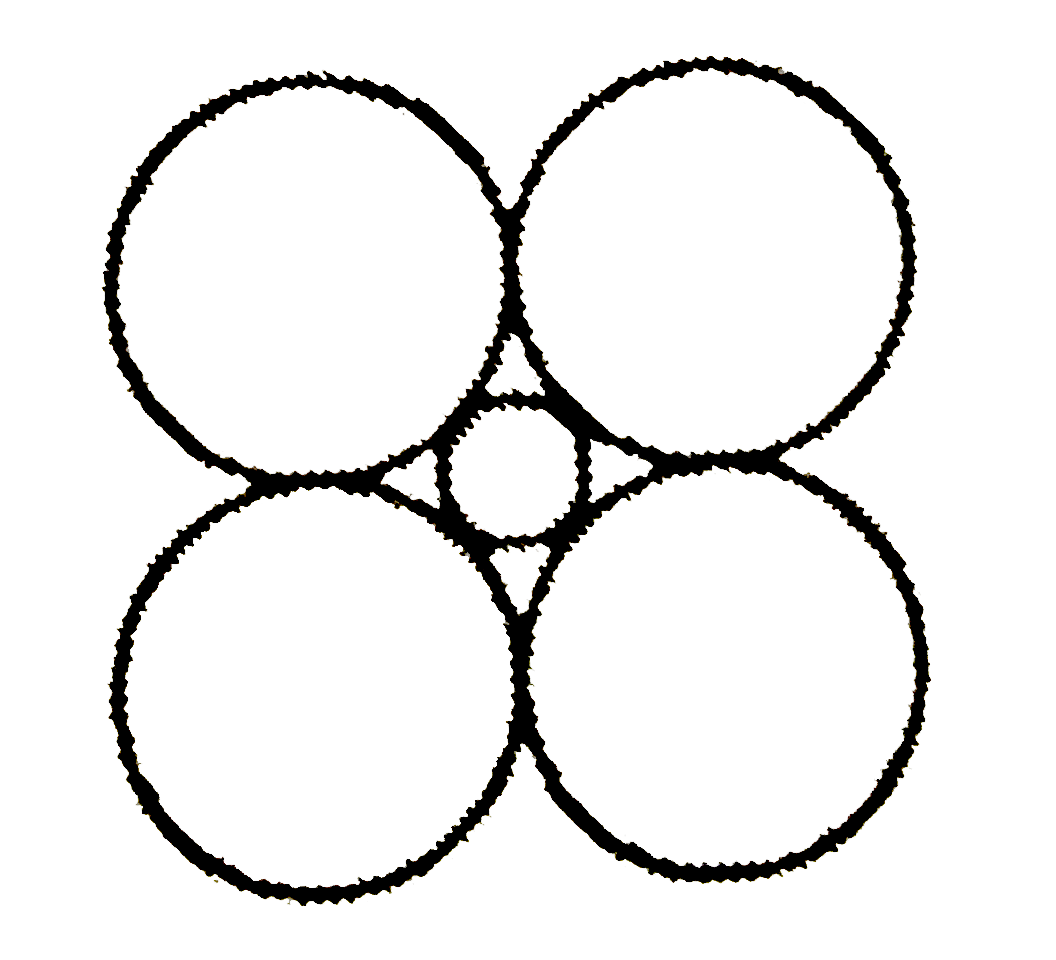
View SolutionFind the equation of the circles which touch 2x−3y+1=0 at (1,1) and having radius √13.
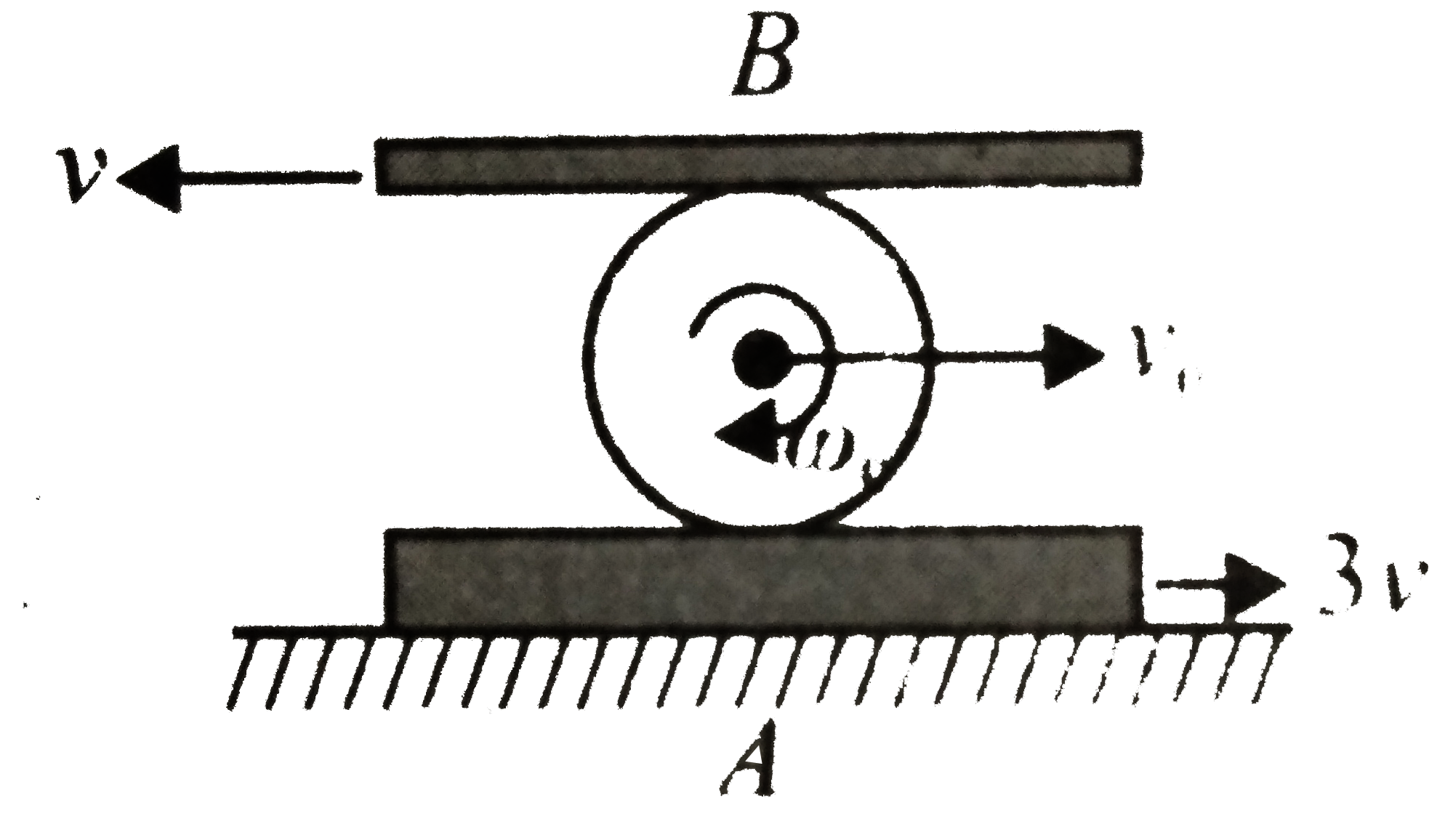
View SolutionThe disc of radius r is confined to roll without slipping at A and B. If the plates have the velocities shown, then
View SolutionIf |z|<1,then1+2z lies (A) on or inside circle having center at origin and radius 2 (B) outside the circle having center at origin and radius 2 (C) inside the circle having center at (1,0) and radius 2 (D) outside the circle having center at (1,0) and radius 2.
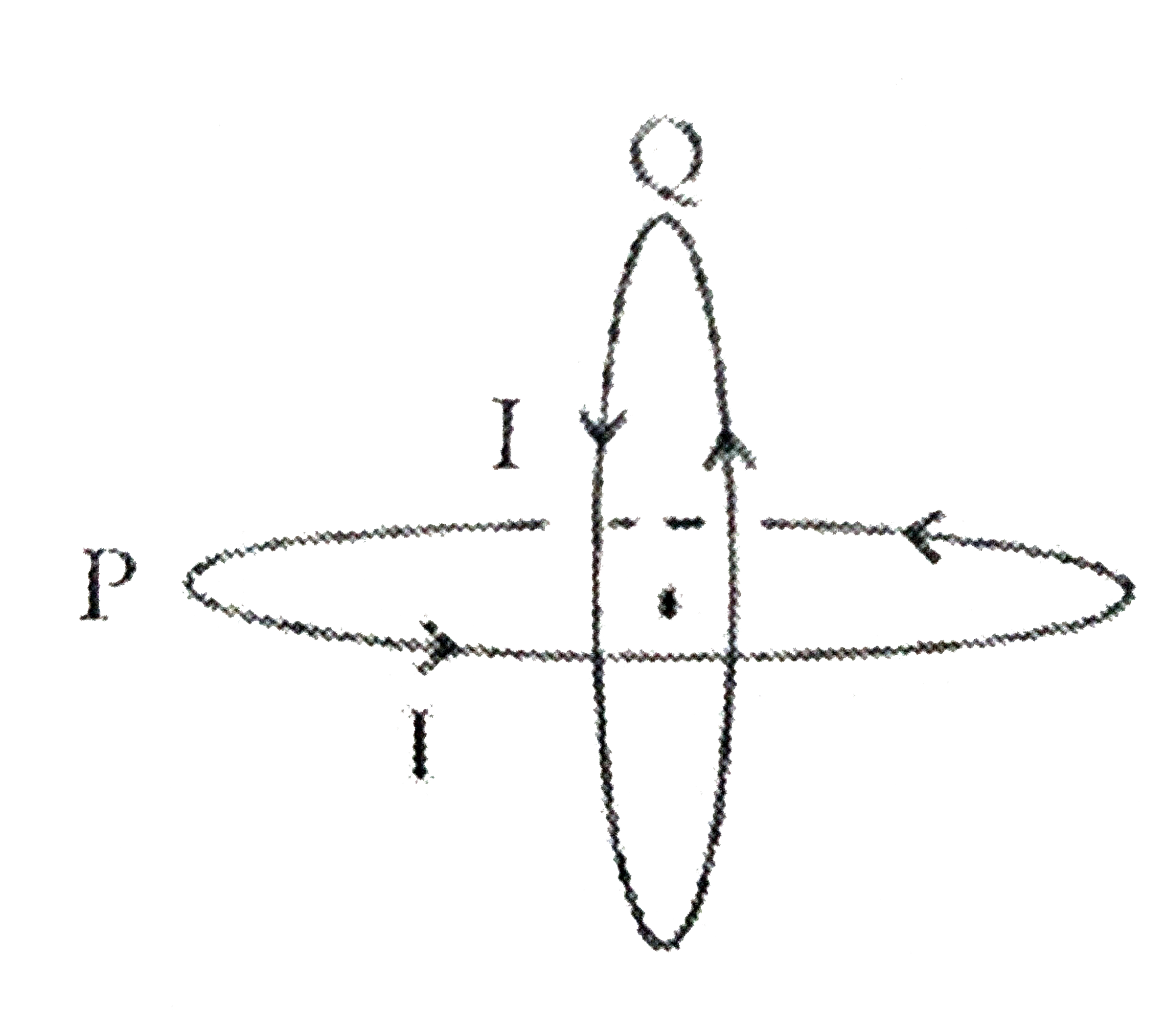
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
View SolutionTwo circles, each of radius 5, have a common tangent at (1, 1) whose equation is 3x+4y−7=0. Then their centres, are
View Solution