In the quadrilateral ABCD, the diagonals AC and BD are equal and perpendicular to each other. What type of a quadrilateral is ABCD?
To determine the type of quadrilateral ABCD given that its diagonals AC and BD are equal and perpendicular to each other, we can follow these steps:
1. Understanding the Properties of Quadrilaterals:
In a quadrilateral, if the diagonals are equal and perpendicular, it suggests certain properties about the shape. Common quadrilaterals with these properties include squares and rectangles.
Hint: Recall the properties of different quadrilaterals and their diagonals.
2. Visualizing the Quadrilateral:
Draw a diagram of quadrilateral ABCD with diagonals AC and BD intersecting at point O. Label the lengths of the diagonals as AC = BD.
Hint: Sketching helps in visualizing the relationships between the sides and angles.
3. Congruent Triangles:
Since diagonals AC and BD are equal and intersect at point O, we can form triangles AOB, AOD, BOC, and COD. By the properties of triangles:
- Triangle AOB is congruent to triangle COD (by SAS: Side-Angle-Side).
- Triangle AOD is congruent to triangle BOC (by SAS).
Hint: Use the properties of congruent triangles to establish relationships between the sides and angles.
4. Analyzing Angles:
Since the diagonals are perpendicular, angles AOB and AOD are both 90 degrees. This means that all angles in the triangles formed are right angles.
Hint: Remember that if two lines are perpendicular, they form right angles.
5. Equal Sides:
From the congruence of triangles, we can conclude that:
- OA = OC and OB = OD.
This indicates that the diagonals bisect each other.
Hint: Diagonals that bisect each other are a key characteristic of certain quadrilaterals.
6. Conclusion:
Since ABCD has equal diagonals that bisect each other and are perpendicular, it fulfills the properties of a square. Therefore, quadrilateral ABCD is a square.
Hint: Check the definitions and properties of squares to confirm your conclusion.
Final Answer
Quadrilateral ABCD is a square.
In a quadrilateral, if the diagonals are equal and perpendicular, it suggests certain properties about the shape. Common quadrilaterals with these properties include squares and rectangles.
Draw a diagram of quadrilateral ABCD with diagonals AC and BD intersecting at point O. Label the lengths of the diagonals as AC = BD.
Since diagonals AC and BD are equal and intersect at point O, we can form triangles AOB, AOD, BOC, and COD. By the properties of triangles:
- Triangle AOB is congruent to triangle COD (by SAS: Side-Angle-Side).
- Triangle AOD is congruent to triangle BOC (by SAS).
Since the diagonals are perpendicular, angles AOB and AOD are both 90 degrees. This means that all angles in the triangles formed are right angles.
From the congruence of triangles, we can conclude that:
- OA = OC and OB = OD.
This indicates that the diagonals bisect each other.
Since ABCD has equal diagonals that bisect each other and are perpendicular, it fulfills the properties of a square. Therefore, quadrilateral ABCD is a square.
Quadrilateral ABCD is a square.
Topper's Solved these Questions
- TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS EXERCISE - Multiple Correct Answers Type
6 Videos
- VECTORS TRIPLE PRODUCTS, RECIPROCAL SYSTEM OF VECTORSBOOK - CENGAGE ENGLISHCHAPTER - VECTORS TRIPLE PRODUCTS, RECIPROCAL SYSTEM OF VECTORSEXERCISE - DPP 2.4
20 Videos
Similar Questions
Knowledge Check
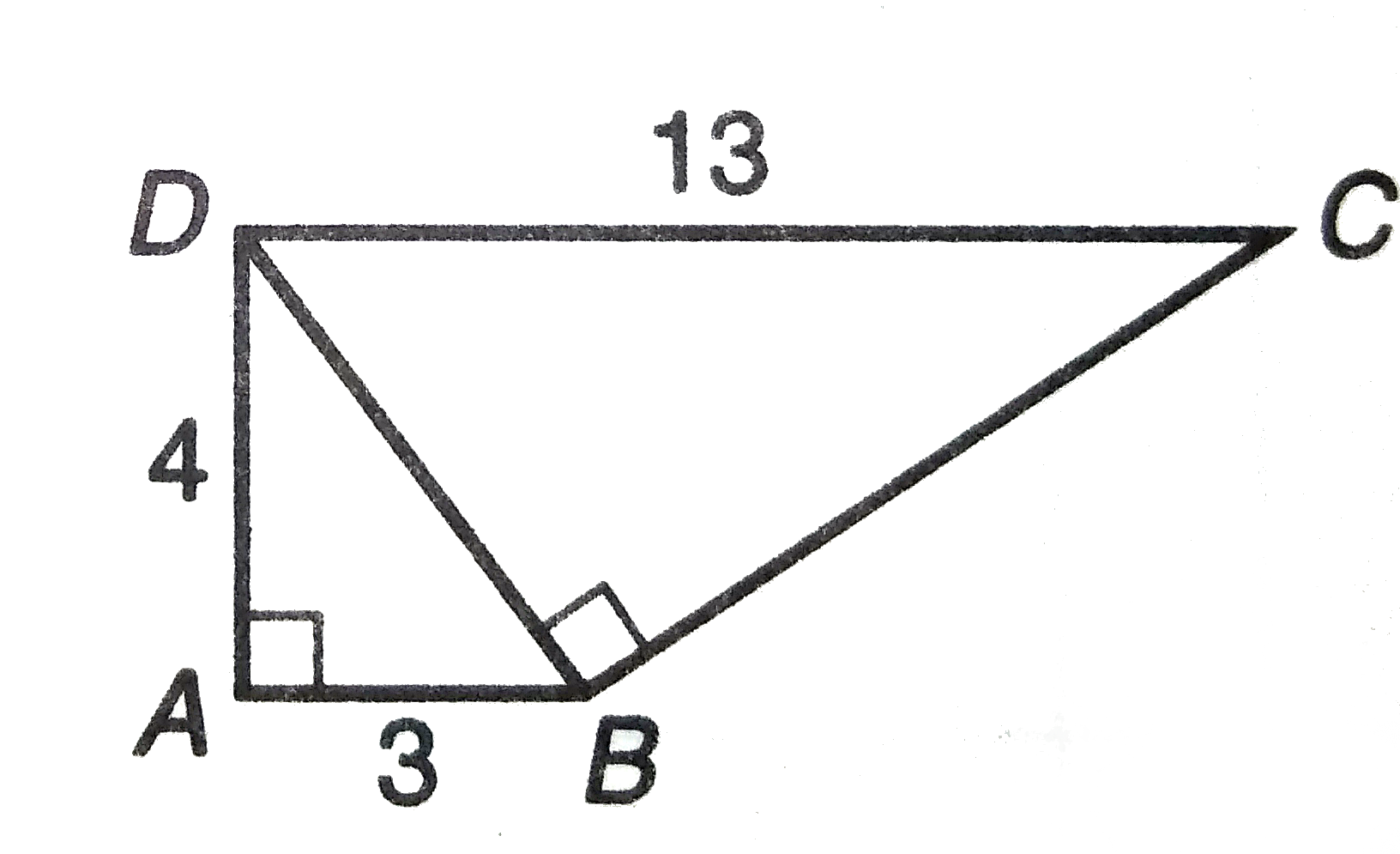
In the figure above, what is the area of quadrilateral ABCD?A28B32C36D42
In a quadrilateral ABCD, −−→AB+−−→DC=
View SolutionIn a quadrilateral ABCD, AB= AD and CB= CD. Prove that:
AC is perpendicular bisector of BD
View SolutionIn quadrilateral ABCD, the diagonals AC and BD intersect each other at point O.
If AO = 2CO and BO = 2DO, show that:
ΔAOB is similar to ΔCOD.
View SolutionIf the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
View SolutionIn quadrilateral ABCD, AB=DC and AD=BC. Prove that the sides AB and DC are parallel to each other.
View SolutionIn quadrilateral ABCD, the diagonals AC and BD intersect each other at point O.
If AO = 2CO and BO = 2DO, show that:
OA×OD=OB×OC.
View SolutionState True or False
If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.
View Solution
