A water jet from a function reaches it maximum height of 4 m at a distance 0.5 m from the vertical passing through the point O of water outlet. The height of the jet above the horizontal OX at a distance of 0.75 m from the point O is 5 m (b) 6 m (c) 3 m (d) 7 m
To solve the problem, we will derive the equation of the parabola representing the water jet and then find the height of the jet at a distance of 0.75 m from the outlet.
1. Understanding the Problem:
We know that the maximum height of the water jet is 4 m at a horizontal distance of 0.5 m from the outlet. We need to find the height of the jet at a distance of 0.75 m.
2. Setting Up the Coordinate System:
Let the origin O be at the water outlet. The x-axis represents the horizontal distance from the outlet, and the y-axis represents the height of the water jet. The point where the maximum height occurs is (0.5,4).
3. Formulating the Parabola:
The general form of a parabola that opens downwards can be given as:
y=a(x−r)(x−s)
where r and s are the x-intercepts of the parabola. In this case, we can assume the x-intercepts are r=0 and s=1. Thus, the equation simplifies to:
y=a(x)(x−1)
4. Finding the Value of a:
We know that at x=0.5, y=4. Substituting these values into the equation:
4=a(0.5)(0.5−1)
This simplifies to:
4=a(0.5)(−0.5)⟹4=−0.25a⟹a=−16
5. Final Equation of the Parabola:
Substituting the value of a back into the equation gives:
y=−16x(x−1)=−16x2+16x
6. Finding the Height at x=0.75:
Now we need to find the height of the jet at x=0.75:
y=−16(0.75)2+16(0.75)
Calculating (0.75)2=0.5625:
y=−16(0.5625)+12=−9+12=3
7. Conclusion:
The height of the jet above the horizontal line at a distance of 0.75 m from the point O is 3 m.
Answer:
(c) 3 m
We know that the maximum height of the water jet is 4 m at a horizontal distance of 0.5 m from the outlet. We need to find the height of the jet at a distance of 0.75 m.
Let the origin O be at the water outlet. The x-axis represents the horizontal distance from the outlet, and the y-axis represents the height of the water jet. The point where the maximum height occurs is (0.5,4).
The general form of a parabola that opens downwards can be given as:
y=a(x−r)(x−s)
where r and s are the x-intercepts of the parabola. In this case, we can assume the x-intercepts are r=0 and s=1. Thus, the equation simplifies to:
y=a(x)(x−1)
We know that at x=0.5, y=4. Substituting these values into the equation:
4=a(0.5)(0.5−1)
This simplifies to:
4=a(0.5)(−0.5)⟹4=−0.25a⟹a=−16
Substituting the value of a back into the equation gives:
y=−16x(x−1)=−16x2+16x
Now we need to find the height of the jet at x=0.75:
y=−16(0.75)2+16(0.75)
Calculating (0.75)2=0.5625:
y=−16(0.5625)+12=−9+12=3
The height of the jet above the horizontal line at a distance of 0.75 m from the point O is 3 m.
(c) 3 m
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions
886 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
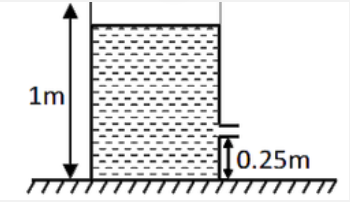
If a small orifice is made at a height of 0.25 m from the ground, the horizontal range of water stream will be : -
View SolutionA body is thrown vertically upward from a point A 125 m above the ground. It goes up to a maximum height of 250 m above the ground and passes through A on its downward journey. The velocity of the body when it is at a height of 70 m above the ground is (g=10m/s2)
View SolutionA body is thrown vertically up reaches a maximum height of 78.4 m. After what time it will reach the ground from the maximum height reached ?
View SolutionA ball thrown up from the ground reaches a maximum height of 20m Find:
a. Its initial velocity.
b. The time taken to reach the highest point.
c. Its velocity just before hitting the ground.
d. Its displacement between 0.5m above the ground.
View SolutionThe maximum vertical distance through which an astronaut can jump on the earth is 0.5 m. Estimate the corresponding distance on the moon.
View SolutionA pole of height 4 m is kept in front of a vertical plane mirror
of length 2m. The lower end of the mirror is at a height of 6m form the grown
.the horizontal distance betweem the mirror and the pole is 2m. Upto what
minimum and maximum heights a man can see the image of top of the pole at a
horizontal distance of 4m (from the mirror O standing on the same horizontal
line which is passing through the pole and the horizontal point below the
mirror?

View SolutionTwo point masses m and 4 m are seperated by a distance d on a line . A third point mass m0 is to be placed at a point on the line such that the net gravitational force on it zero .

The distance of that point from the m mass is
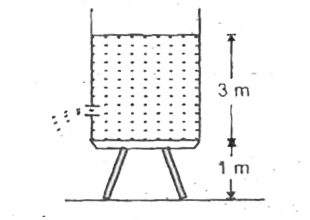
View SolutionWater is filled in a tank upto 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
View SolutionThe intensity of sound from a point source is 1.0×10−8Wm−2, at a distance of 5.0 m from the source. What will be the intensity at a distance of 25 m from the source ?
View SolutionFrom the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is (a) 25 m (b) 50 m (c) 75 m (d) 100 m
View Solution
