If a triangle is inscribed in an ellipse and two of its sides are parallel to the given straight lines, then prove that the third side touches the fixed ellipse.
To prove that the third side of a triangle inscribed in an ellipse touches the fixed ellipse when two of its sides are parallel to given straight lines, we can follow these steps:
Step 1: Understand the Configuration
Let the triangle be PQR inscribed in the ellipse. We know that two sides, say PQ and PR, are parallel to given straight lines.
Step 2: Define Angles
Let the angles at vertices P,Q,R be θ1,θ2,θ3 respectively.
Step 3: Write the Equations of the Sides
The equations of the sides PQ and PR can be expressed in terms of the angles:
- For side PQ:
xacos(θ1+θ22)+ybsin(θ1+θ22)=cos(θ1−θ22)
- For side PR:
xacos(θ2+θ32)+ybsin(θ2+θ32)=cos(θ2−θ32)
Step 4: Set Up Parallel Conditions
Since PQ and PR are parallel to the given straight lines, we can set:
- θ1+θ2=2α
- θ2+θ3=2β
Step 5: Subtract the Equations
Subtract the two equations to find a relationship between θ2 and θ3:
θ2−θ3=2(α−β)
Step 6: Write the Equation of Side QR
Now, we can write the equation for side QR:
xacos(θ2+θ32)+ybsin(θ2−θ32)=cos(θ2−θ32)
Step 7: Substitute the Relationship
Substituting θ2−θ3=2(α−β) into the equation for side QR:
xacos(θ2+θ32)+ybsin(α−β)=cos(α−β)
Step 8: Relate to the Ellipse Equation
The equation of the fixed ellipse is given by:
x2a2+y2b2=1
By manipulating the equations, we can show that the equation of line QR is tangent to the ellipse.
Conclusion
Thus, we have shown that the third side QR touches the fixed ellipse when two sides of the triangle are parallel to the given straight lines.
---
Let the triangle be PQR inscribed in the ellipse. We know that two sides, say PQ and PR, are parallel to given straight lines.
Let the angles at vertices P,Q,R be θ1,θ2,θ3 respectively.
The equations of the sides PQ and PR can be expressed in terms of the angles:
- For side PQ:
xacos(θ1+θ22)+ybsin(θ1+θ22)=cos(θ1−θ22)
- For side PR:
xacos(θ2+θ32)+ybsin(θ2+θ32)=cos(θ2−θ32)
Since PQ and PR are parallel to the given straight lines, we can set:
- θ1+θ2=2α
- θ2+θ3=2β
Subtract the two equations to find a relationship between θ2 and θ3:
θ2−θ3=2(α−β)
Now, we can write the equation for side QR:
xacos(θ2+θ32)+ybsin(θ2−θ32)=cos(θ2−θ32)
Substituting θ2−θ3=2(α−β) into the equation for side QR:
xacos(θ2+θ32)+ybsin(α−β)=cos(α−β)
The equation of the fixed ellipse is given by:
x2a2+y2b2=1
By manipulating the equations, we can show that the equation of line QR is tangent to the ellipse.
Thus, we have shown that the third side QR touches the fixed ellipse when two sides of the triangle are parallel to the given straight lines.
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions
886 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
A triangle is inscribed in the hyperbola xy=c2 and two of its sides are parallel to y=m1xandy=m2x. Prove that the third side touches the hyperbola 4m1m2xy=c2(m1+m2)2.
View SolutionFind the length of the third side of the triangle.
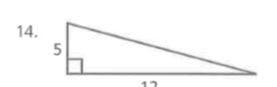
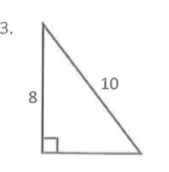
View SolutionFind the length of the third side of the triangle.
View SolutionAn equilateral triangle is inscribed in an ellipse whose equation is x2+4y2=4 If one vertex of the triangle is (0,1) then the length of each side is
View SolutionAn equilateral triangle is inscribed in a circle of radius 6cm. Find its side.
View SolutionProve that any two sides of a triangle are together greater than twice the median drawn to the third side.
View SolutionIf a triangle is inscribed in a circle, then prove that the product of any two sides of the triangle is equal to the product of the diameter and the perpendicular distance of the thrid side from the opposite vertex.
View SolutionAn equilateral triangle is inscribed in the parabola y2=8x with one of its vertices is the vertex of the parabola. Then, the length or the side or that triangle is
View SolutionTheorem 6.2 : If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
View SolutionThe line drawn through the mid-point of one side of a triangle, parallel to another side, intersects the third side at its mid-point.
View Solution
