Consider the graphs ofy=Ax2andy2+3=x2+4y, where A is a positive constant and x,y∈R.Number of points in which the two graphs intersect, is
To find the number of points in which the graphs of y=Ax2 and y2+3=x2+4y intersect, we can follow these steps:
Step 1: Rewrite the equations
We have two equations:
1. y=Ax2
2. y2+3=x2+4y
We can rearrange the second equation:
y2−4y+3=x2
This can be factored as:
(y−1)(y−3)=x2
Step 2: Substitute y=Ax2 into the second equation
Now, we substitute y=Ax2 into the rearranged second equation:
(Ax2−1)(Ax2−3)=x2
Step 3: Expand the equation
Expanding the left-hand side gives:
Ax4−3Ax2−Ax2+3=x2
This simplifies to:
Ax4−(4A+1)x2+3=0
Step 4: Let z=x2
Let z=x2, then we have a quadratic equation in z:
Az2−(4A+1)z+3=0
Step 5: Find the discriminant
To determine the number of solutions for z, we calculate the discriminant D of the quadratic equation:
D=b2−4ac=(−(4A+1))2−4⋅A⋅3
D=(4A+1)2−12A
D=16A2+8A+1−12A
D=16A2−4A+1
Step 6: Analyze the discriminant
The discriminant D is a quadratic in A. We need to determine when D≥0 to find the number of real solutions for z:
D=16A2−4A+1
The discriminant of this quadratic can be calculated:
D′=(−4)2−4⋅16⋅1=16−64=−48
Since the discriminant D′<0, the quadratic 16A2−4A+1 is always positive. Therefore, D≥0 for all positive A.
Step 7: Conclusion on the number of intersections
Since the discriminant D is always positive, the quadratic in z will have two distinct real roots. Each root corresponds to two values of x (since z=x2 can be positive or negative), leading to a total of four intersection points.
Thus, the number of points in which the two graphs intersect is:
4
We have two equations:
1. y=Ax2
2. y2+3=x2+4y
y2−4y+3=x2
This can be factored as:
(y−1)(y−3)=x2
Now, we substitute y=Ax2 into the rearranged second equation:
(Ax2−1)(Ax2−3)=x2
Expanding the left-hand side gives:
Ax4−3Ax2−Ax2+3=x2
This simplifies to:
Ax4−(4A+1)x2+3=0
Let z=x2, then we have a quadratic equation in z:
Az2−(4A+1)z+3=0
To determine the number of solutions for z, we calculate the discriminant D of the quadratic equation:
D=b2−4ac=(−(4A+1))2−4⋅A⋅3
D=(4A+1)2−12A
D=16A2+8A+1−12A
D=16A2−4A+1
The discriminant D is a quadratic in A. We need to determine when D≥0 to find the number of real solutions for z:
D=16A2−4A+1
The discriminant of this quadratic can be calculated:
D′=(−4)2−4⋅16⋅1=16−64=−48
Since the discriminant D′<0, the quadratic 16A2−4A+1 is always positive. Therefore, D≥0 for all positive A.
Since the discriminant D is always positive, the quadratic in z will have two distinct real roots. Each root corresponds to two values of x (since z=x2 can be positive or negative), leading to a total of four intersection points.
4
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBook:CENGAGE ENGLISHChapter:COMPLEX NUMBERS AND QUADRATIC EQUATIONSExercise:All Questions
Explore 886 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Book:CENGAGE ENGLISHChapter:DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Exercise:Multiple correct answers type
Explore 11 Videos
Similar Questions
Knowledge Check
Which is the graph of y=−(x−2)2 ?
A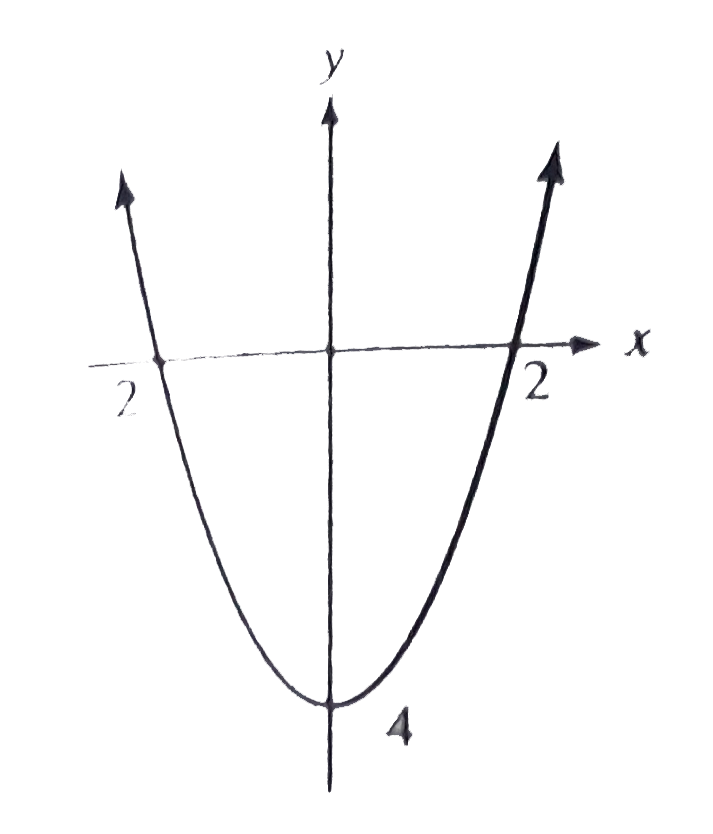 B
B C
C D
D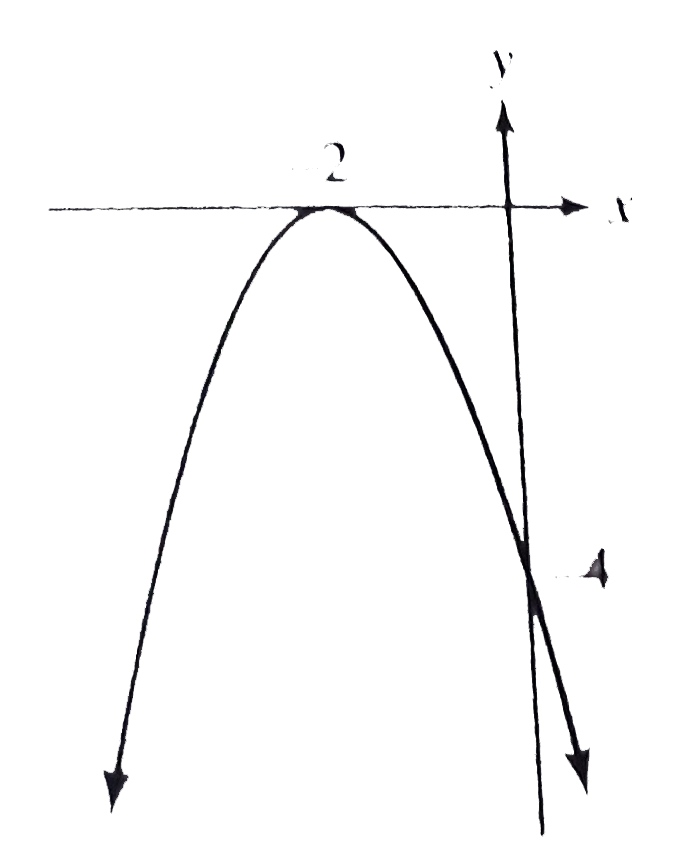
The graph of x2=(2y+3)2 is
Aan ellipseBa parabolaCa hyperbolaDintersecting linesThe graphs of y=2x-5 and x + 3y=-1 intersect at
A(-1,2)B(-2,-1)C(2,-1)D(-2,1)
Draw the graph of y=2x3−15x2+36x+12 y=−x4+2x2−3
View SolutionProve that graphs of y=x2+2andy=3x−4 never intersect.
View SolutionConsider the two graphs y=2x and x2−xy+2y2=28. The absolute value of the tangent of the angle between the two curves at the points where they meet, is ……………
View SolutionFind the points at which the graphs of y=12x2−3 and y=x +1 intersect.
View SolutionThe graph of y=log5xandy=ln 0.5x intersect at a point where x equals
View Solution