Question

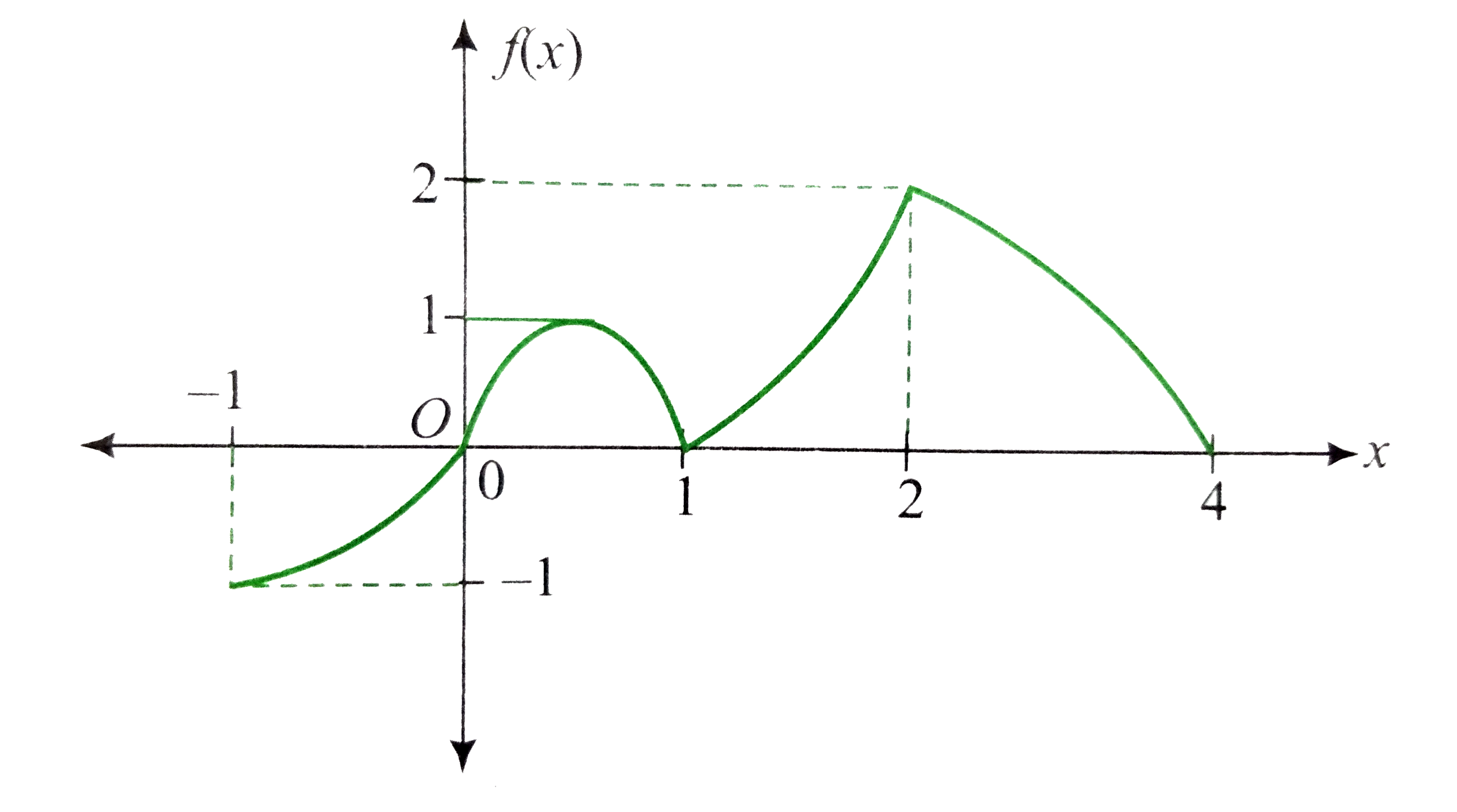
The graph of a function fx) which is defined in [-1, 4] is shown in the adjacent figure. Identify the correct statement(s). (1) domain of $f\left(\left|x\right|\right)-1)is[-5,5]$ (2) range of $f(\left|x\right|+1)$ is $[0,2]$ (3) range of $f(-\left|x\right|)$ is [-1,0] (4) domain of $f\left(\left|x\right|\right)is[-3,3]$

Explanation

To solve the problem, we need to analyze the statements about the function $$f\left(x\right)$$ defined on the interval $$(-1,4)$$ based on the provided graph. Let's evaluate each statement step by step.

Step 1: Analyze the Domain of \( f(|x|) - 1 \)

1. The function \( f(x) \) is defined for \( x \in (-1, 4) \).
2. The expression \( |x| \) takes values from 0 to 5 when \( x \) is in the range of \((-5, 5)\).
3. Therefore, \( f(|x|) \) will be defined for \( |x| \) values in \((-1, 4)\), which corresponds to \( x \) values in the interval \((-4, 4)\).
4. Since we are looking for \( f(|x|) - 1 \), the domain remains the same, which is \((-4, 4)\).

Conclusion: The domain of \( f(|x|) - 1 \) is \((-4, 4)\), not \((-5, 5)\).

Step 2: Analyze the Range of \( f(|x| + 1) \)

1. The expression \( |x| + 1 \) takes values from 1 to 5 when \( x \) is in the range of \((-4, 4)\).
2. The function \( f(x) \) is defined from \((-1, 4)\) and takes values from \((-1, 2)\).
3. For \( |x| + 1 \), the minimum value is 1 (when \( x = 0 \)) and the maximum value is 5 (when \( x = 4 \)).
4. Therefore, we need to evaluate \( f(x) \) for \( x \) in the range \((1, 4)\).
5. The corresponding range of \( f(x) \) for \( x \in (1, 4) \) is from \( f(1) \) to \( f(4) \). Assuming \( f(1) \) is 0 and \( f(4) \) is 2, the range of \( f(|x| + 1) \) is \((0, 2)\).

Conclusion: The range of \( f(|x| + 1) \) is \((0, 2)\).

Step 3: Analyze the Range of \( f(-|x|) \)

1. The expression \( -|x| \) takes values from 0 to -5 when \( x \) is in the range of \((-5, 5)\).
2. The function \( f(x) \) is defined from \((-1, 4)\) and takes values from \((-1, 2)\).
3. For \( -|x| \), the maximum value is 0 (when \( x = 0 \)) and the minimum value is -5 (when \( x = 5 \)).
4. Therefore, we need to evaluate \( f(x) \) for \( x \) in the range \((-1, 0)\).
5. The corresponding range of \( f(x) \) for \( x \in (-1, 0) \) is from \( f(-1) \) to \( f(0) \). Assuming \( f(-1) \) is -1 and \( f(0) \) is 0, the range of \( f(-|x|) \) is \((-1, 0)\).

Conclusion: The range of \( f(-|x|) \) is \((-1, 0)\).

Step 4: Analyze the Domain of \( f(|x|) \)

1. The expression \( |x| \) takes values from 0 to 5 when \( x \) is in the range of \((-5, 5)\).
2. The function \( f(x) \) is defined from \((-1, 4)\).
3. Therefore, \( |x| \) must be in the range \((-1, 4)\), which corresponds to \( x \) values in the interval \((-4, 4)\).

Conclusion: The domain of \( f(|x|) \) is \((-4, 4)\), not \((-3, 3)\).

Final Summary of Statements

1. Domain of \( f(|x|) - 1 \) is \((-5, 5)\) - Incorrect
2. Range of \( f(|x| + 1) \) is \((0, 2)\) - Correct
3. Range of \( f(-|x|) \) is \((-1, 0)\) - Correct
4. Domain of \( f(|x|) \) is \((-3, 3)\) - Incorrect

Correct Statements
- Statement 2 and Statement 3 are correct.