Solve
Video Solution
Text Solution
We have
or
Roots of equation are values of x where the graphs of
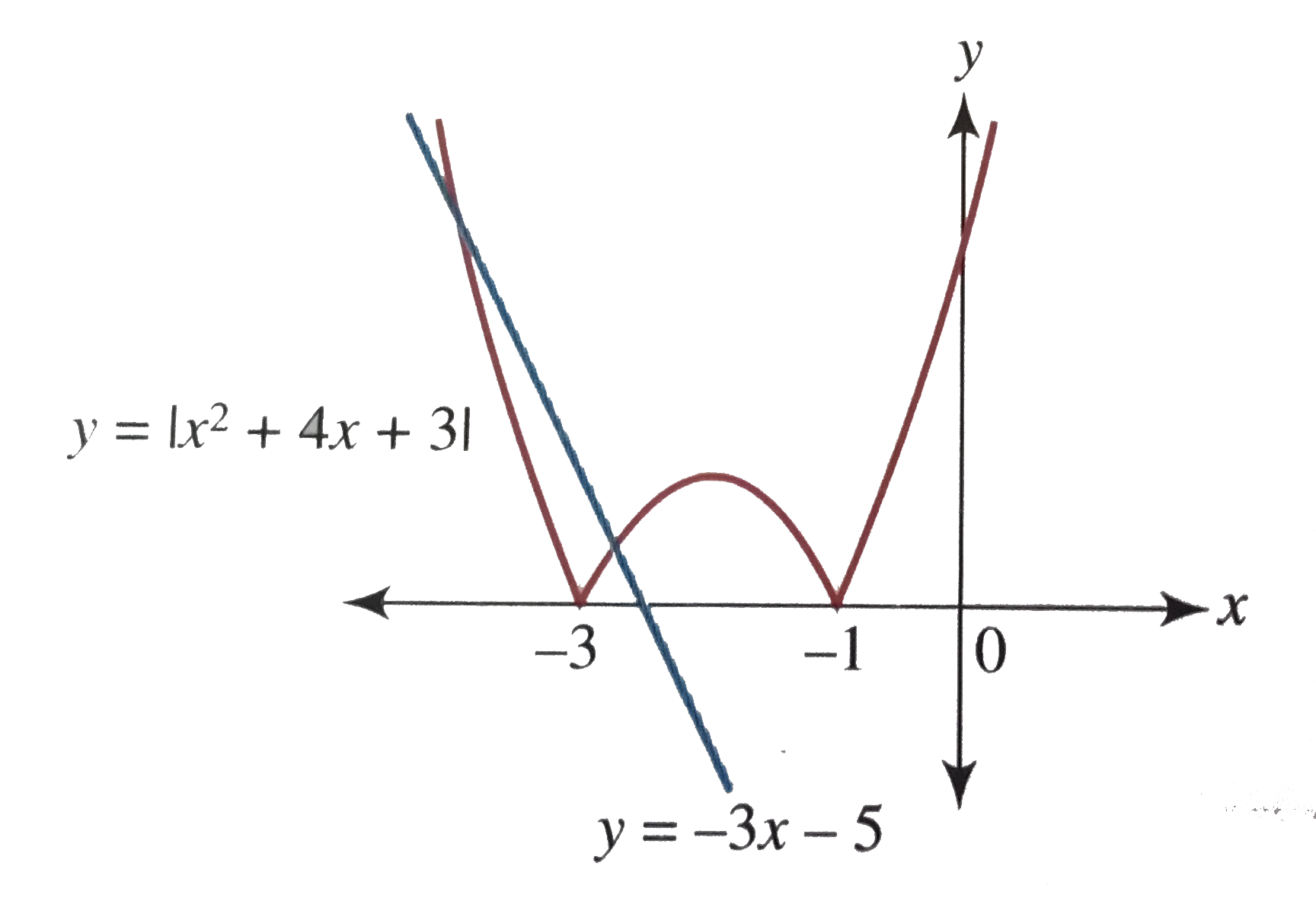
From the graph, one root and one root for .
For ,
or
For ,
Hence
|
Topper's Solved these Questions
Similar Questions
Solve x2−4|x|+3<0.
View SolutionSolve x2−4|x|+3<0.
View SolutionSolve x2+3x+5=0
View SolutionSolve x|2x+3∣+4=5
View Solutionsolve x2+2x+4=0
View SolutionSolve x3−2x2+2x−4=0.
View SolutionSolve: 6x2+ 13x−42x+5=12x2+5x−24x+3
View SolutionSolve: 3x−4y−1=02x−83y+5=0
View SolutionSolve : 2x2−3x+5<0
View SolutionSolve for x |x−2,2x−3,3x−4,x−4,2x−9,3x−16,x−8,2x−27,3x−64|=0.
View Solution
