Shortest distance between the lines x−11=y−11=z−11andx−21=y−31=z−41 is equal to
√14
√7
√2
none of these
The correct Answer is:c
To find the shortest distance between the two given lines, we can use the formula for the distance between two parallel lines in three-dimensional space. The lines are given in symmetric form:
1. Line 1: (x−1)/1=(y−1)/1=(z−1)/1
2. Line 2: (x−2)/1=(y−3)/1=(z−4)/1
Step 1: Identify Points and Direction Ratios
From the equations of the lines, we can identify:
- For Line 1, a point on the line P1(1,1,1) and the direction ratios a1=1,b1=1,c1=1.
- For Line 2, a point on the line P2(2,3,4) and the direction ratios a2=1,b2=1,c2=1.
Step 2: Check if Lines are Parallel
Since the direction ratios of both lines are the same (1,1,1), we conclude that the lines are parallel.
Step 3: Use the Distance Formula for Parallel Lines
The formula for the shortest distance d between two parallel lines is given by:
d=|(P2−P1)⋅(a×b)||a|
Where:
- P1 and P2 are points on the two lines.
- a is the direction vector of the first line.
- b is the direction vector of the second line (which is the same in this case).
Step 4: Calculate the Vector P2−P1
P2−P1=(2−1,3−1,4−1)=(1,2,3)
Step 5: Calculate the Cross Product a×b
Since both direction vectors are the same, we can denote a=(1,1,1).
The cross product a×a is zero, but since we are looking for the distance between two parallel lines, we can directly use the formula for the distance.
Step 6: Calculate the Magnitude of the Direction Vector
|a|=√12+12+12=√3
Step 7: Calculate the Distance
Now, we can use the formula for distance:
1. Calculate the numerator:
|(P2−P1)⋅a|=|(1,2,3)⋅(1,1,1)|=|1⋅1+2⋅1+3⋅1|=|1+2+3|=|6|=6
2. Now substitute into the distance formula:
d=6√3=2√3
Final Answer
The shortest distance between the two lines is 2√3.
---
2. Line 2: (x−2)/1=(y−3)/1=(z−4)/1
From the equations of the lines, we can identify:
- For Line 1, a point on the line P1(1,1,1) and the direction ratios a1=1,b1=1,c1=1.
- For Line 2, a point on the line P2(2,3,4) and the direction ratios a2=1,b2=1,c2=1.
Since the direction ratios of both lines are the same (1,1,1), we conclude that the lines are parallel.
The formula for the shortest distance d between two parallel lines is given by:
- P1 and P2 are points on the two lines.
- a is the direction vector of the first line.
- b is the direction vector of the second line (which is the same in this case).
P2−P1=(2−1,3−1,4−1)=(1,2,3)
Since both direction vectors are the same, we can denote a=(1,1,1).
|a|=√12+12+12=√3
Now, we can use the formula for distance:
|(P2−P1)⋅a|=|(1,2,3)⋅(1,1,1)|=|1⋅1+2⋅1+3⋅1|=|1+2+3|=|6|=6
d=6√3=2√3
The shortest distance between the two lines is 2√3.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CORRECT ANSWER TYPE17videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - REASONING TYPE10videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - SUBJECTIVE TYPE17videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions294videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)1videos
TRIGONOMETRIC EQUATIONS
Similar Questions
The shortest distance between the lines
x−12=y−13=z+26andx−24=y+11=z−37View SolutionFind the shortest distance between the lines x−12=y−23=z−34andx−23=y−44=z−55 .
View SolutionFind the shortest distance between the lines x−12=y−23=z−34andx−23=y−44=z−55 .
View SolutionFind the shortest distance between the lines x−12=y−23=z−34andx−23=y−44=z−55 .
View SolutionFind the shortest distance between the lines x−12=y−23=z−34andx−23=y−44=z−55 .
View SolutionStatement 1: The shortest distance between the lines x−3=y−11=z+1−1andx−21=y−32=(z+(13/7)−1)is zero. Statement 2: The given lines are perpendicular.
View SolutionFor an ideal gas, an illustration of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
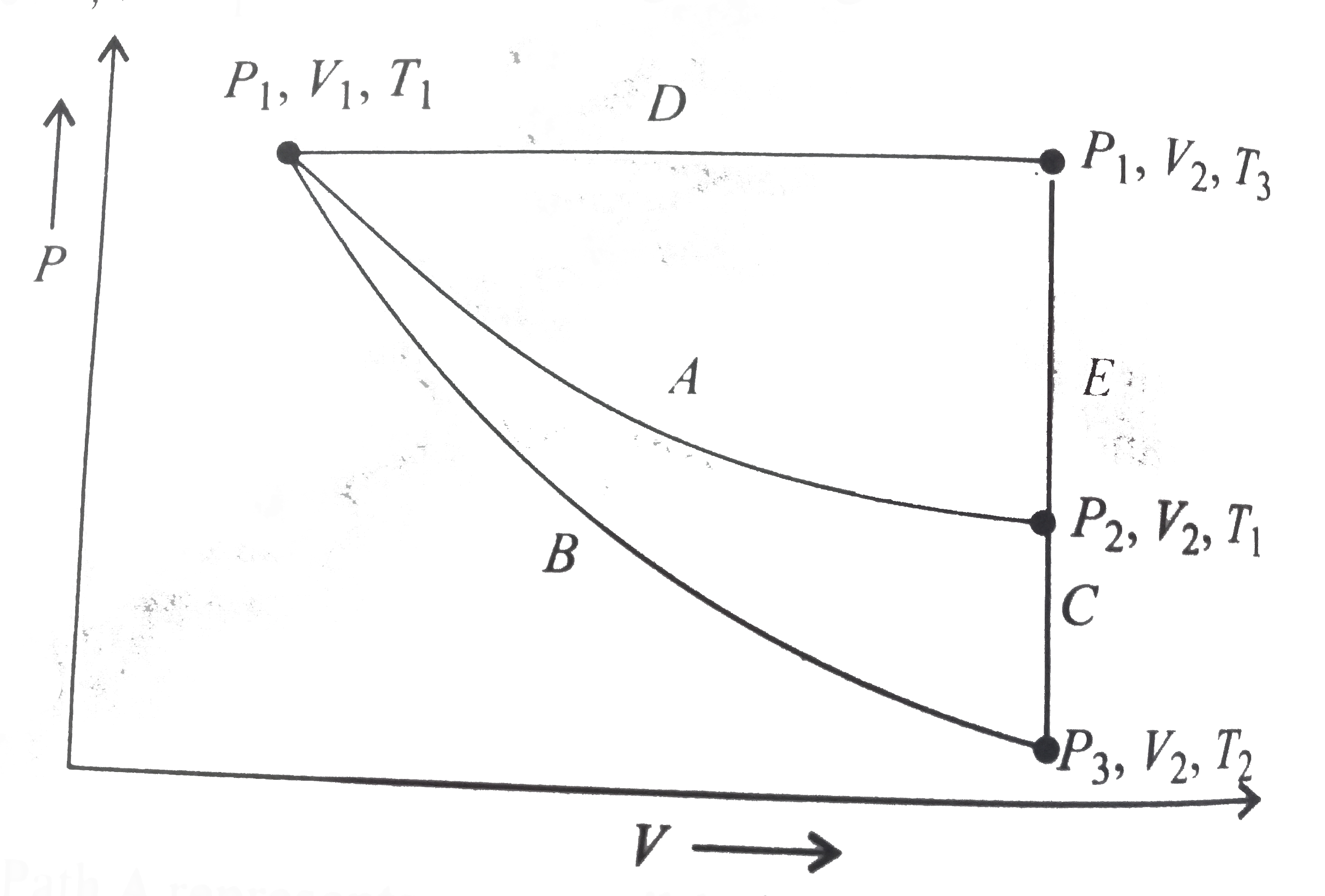
Path A represents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path (D+E)?View SolutionFind the length of the shortest distance between the lines x−12=y−43=z+1−3andx−41=y−33=z−22
View SolutionThe shortest distance between the lines x−33=y−8−1=z−31andx+3−3=y+72=z−64 is a. √30 b. 2√30 c. 5√30 d. 3√30
View SolutionThe shortest distance between the lines x−33=y−8−1=z−31andx+3−3=y+72=z−64 is a. √30 b. 2√30 c. 5√30 d. 3√30
View Solution

