The equation of two straight lines are x−12=y+31=z−2−3andx−21=y−1−3=z+32. Statement 1: the given lines are coplanar. Statement 2: The equations 2r−s=1,r+3s=4and3r+2s=5 are consistent.
Both the statements are true, and Statement 2 is the correct explanation for Statement 1.
Both the Statements are true, but Statement 2 is not the correct explanation for Statement 1.
Statement 1 is true and Statement 2 is false.
Statement 1 is false and Statement 2 is true.
The correct Answer is:d
To determine whether the given lines are coplanar and whether the equations are consistent, we can follow these steps:
Step 1: Write the equations of the lines in parametric form
The equations of the two lines are given as:
1. Line 1: (x−1)/2=(y+3)/1=(z−2)/(−3)
2. Line 2: (x−2)/1=(y−1)/(−3)=(z+3)/2
Let’s express these in parametric form.
For Line 1, let r be the parameter:
- x=2r+1
- y=r−3
- z=−3r+2
For Line 2, let s be the parameter:
- x=s+2
- y=−3s+1
- z=2s−3
Step 2: Set the equations equal to each other
To find if the lines intersect, we set the parametric equations equal to each other:
1. 2r+1=s+2 (Equation 1)
2. r−3=−3s+1 (Equation 2)
3. −3r+2=2s−3 (Equation 3)
Step 3: Rearranging the equations
From Equation 1:
2r−s=1(Equation 1)
From Equation 2:
r+3s=4(Equation 2)
From Equation 3:
3r+2s=5(Equation 3)
Step 4: Solve the equations
Now we will solve the system of equations formed by Equations 1, 2, and 3.
1. From Equation 1: s=2r−1
2. Substitute s in Equation 2:
r+3(2r−1)=4r+6r−3=47r=7r=1
3. Substitute r=1 back into s=2r−1:
s=2(1)−1=1
4. Now substitute r=1 and s=1 into Equation 3 to check for consistency:
3(1)+2(1)=53+2=5(True)
Conclusion
Since all equations are satisfied, the equations are consistent.
Step 5: Check coplanarity
The lines are coplanar if the scalar triple product of the direction vectors and the vector between points on the two lines is zero.
- Direction vector of Line 1: →d1=(2,1,−3)
- Direction vector of Line 2: →d2=(1,−3,2)
- Vector between points on the lines (using points from parametric equations):
→A=(1,−3,2)(from Line 1 when r=0)
→B=(2,1,−3)(from Line 2 when s=0)
→AB=→B−→A=(2−1,1+3,−3−2)=(1,4,−5)
Now calculate the scalar triple product:
→d1⋅(→d2×→AB)=0
If this equals zero, the lines are coplanar.
Final Answer
- Statement 1: The given lines are coplanar (True).
- Statement 2: The equations are consistent (True).
The equations of the two lines are given as:
2. Line 2: (x−2)/1=(y−1)/(−3)=(z+3)/2
- x=2r+1
- y=r−3
- z=−3r+2
- x=s+2
- y=−3s+1
- z=2s−3
To find if the lines intersect, we set the parametric equations equal to each other:
2. r−3=−3s+1 (Equation 2)
3. −3r+2=2s−3 (Equation 3)
From Equation 1:
2r−s=1(Equation 1)
r+3s=4(Equation 2)
3r+2s=5(Equation 3)
Now we will solve the system of equations formed by Equations 1, 2, and 3.
2. Substitute s in Equation 2:
r+3(2r−1)=4r+6r−3=47r=7r=1
s=2(1)−1=1
3(1)+2(1)=53+2=5(True)
Since all equations are satisfied, the equations are consistent.
The lines are coplanar if the scalar triple product of the direction vectors and the vector between points on the two lines is zero.
- Direction vector of Line 2: →d2=(1,−3,2)
- Vector between points on the lines (using points from parametric equations):
→A=(1,−3,2)(from Line 1 when r=0)
→B=(2,1,−3)(from Line 2 when s=0)
→AB=→B−→A=(2−1,1+3,−3−2)=(1,4,−5)
→d1⋅(→d2×→AB)=0
If this equals zero, the lines are coplanar.
- Statement 1: The given lines are coplanar (True).
- Statement 2: The equations are consistent (True).
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - LINKED COMPREHENSION TYPE12videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MATRIX-MATCH TYPE5videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CORRECT ANSWER TYPE17videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions294videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)1videos
TRIGONOMETRIC EQUATIONS
Similar Questions
The equation of two straight lines are x−12=y+31=z−2−3andx−21=y−1−3=z+32. Statement 1: the given lines are coplanar. Statement 2: The equations 2x1−y1=1,x1+3y1=4and3x−1+2y1=5 are consistent.
View SolutionThe equations of two straight lines are
x−12=y+31=z−2−3 and x−21=y−1−3=z+32
Statement 1: The given lines are coplanar.
Statement 2: The equations
2r−s=1
r+3s=4
3r+2s=5
are consistent.View SolutionGiven lines x−42=y+54=z−1−3andx−21=y+13=z2
Statement-I The lines intersect.
Statement-II They are not parallel.View SolutionShow that the lines x−13=y+12=z−15andx+24=y−13=z+1−2 do not intersect.
View SolutionShow that the lines x−13=y+12=z−15andx+24=y−13=z+1−2 do not intersect.
View SolutionFind the shortest distance between the lines x−12=y−23=z−34andx−23=y−44=z−55 .
View SolutionFind the shortest distance between the lines x−12=y−23=z−34andx−23=y−44=z−55 .
View SolutionFind the shortest distance between the lines x−12=y−23=z−34andx−23=y−44=z−55 .
View SolutionFind the shortest distance between the lines x−12=y−23=z−34andx−23=y−44=z−55 .
View SolutionFor an ideal gas, an illustration of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
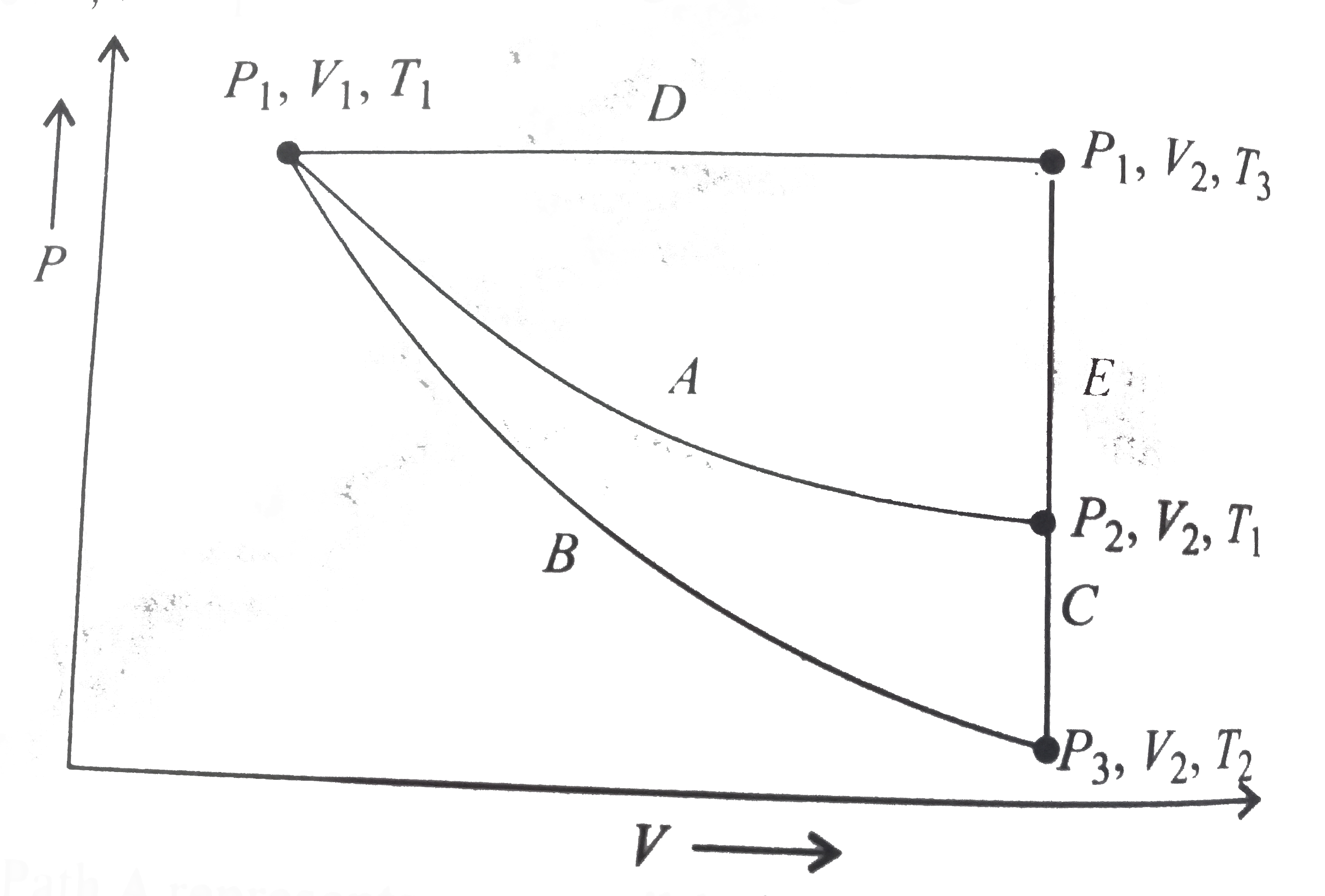
Path A represents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path (D+E)?View Solution

