Question

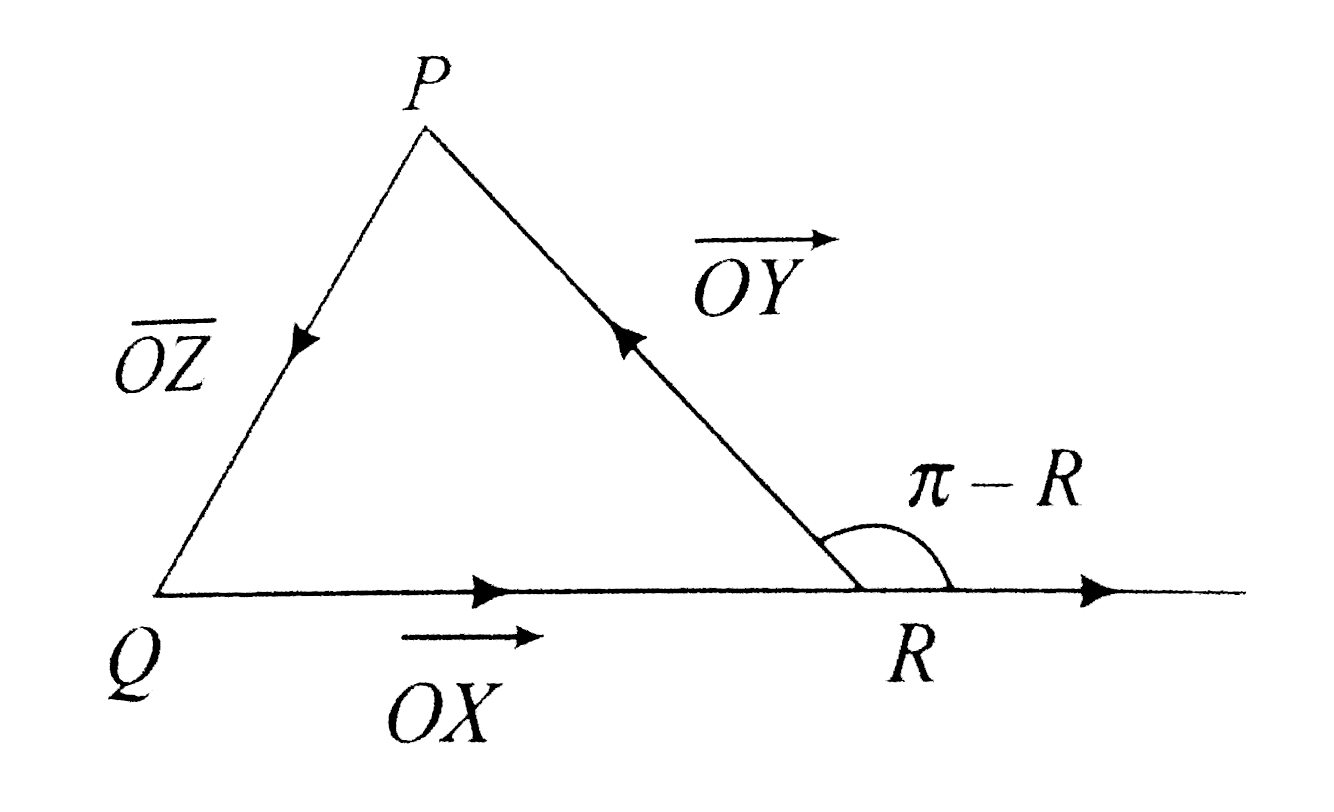
Let $O$
be the origin, and $OXxOY,OZ$
be three unit vectors in the direction of the sides $QR$
, $RP$
, $PQ$
, respectively of a triangle PQR.
If the triangle PQR varies, then the minimum value of $\cos (P+Q)+\cos (Q+R)+\cos (R+P)$
is:
$-\frac{3}{2}$
(b) $\frac{5}{3}$
(c) $\frac{3}{2}$
(d) $-\frac{5}{3}$

Options

A. `-(5)/(3)`
B. `-(3)/(2)`
C. `(3)/(2)`
D. `(5)/(3)`

Answer

B

Explanation

`-(cosP+cosQ+cosR)`
`= vec(OX).vec(OY)+vec(OZ)+vec(OZ).vec(OX)`
`=((vec(OX)+vec(OY)+vec(OZ))^(2)-(|vec(OX)|^(2)+|vec(OY)|^(2)+|vec(OZ)|^(2)))/(2) ge-(3)/(2)`