Out of 100 students, 15 passed in English, 12 passed in Mathmatics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science , 4 in English and Science, 4 in all the three. Find how many passed
(i) in English and Mathematics but not in Science.
(ii) in Mathematics and Science but not in English.
(iii) in Mathematics only.
(iv) in more than one subject only.
The correct Answer is:(a) 2 (b) 3 ( c) 3 (d) 9
To solve the problem step by step, we will use the principle of inclusion-exclusion and a Venn diagram to visualize the data.
Given Data:
- Total students = 100
- Students passed in:
- English (E) = 15
- Mathematics (M) = 12
- Science (S) = 8
- English and Mathematics (E ∩ M) = 6
- Mathematics and Science (M ∩ S) = 7
- English and Science (E ∩ S) = 4
- All three subjects (E ∩ M ∩ S) = 4
Step 1: Fill in the Venn Diagram
1. All three subjects (E ∩ M ∩ S): 4 students passed in all three subjects.
2. English and Mathematics (E ∩ M): 6 students passed in both English and Mathematics. Since 4 of these also passed Science, the number of students who passed only English and Mathematics (E ∩ M but not S) is:
(E∩M)−(E∩M∩S)=6−4=2
3. Mathematics and Science (M ∩ S): 7 students passed in both Mathematics and Science. Since 4 of these also passed English, the number of students who passed only Mathematics and Science (M ∩ S but not E) is:
(M∩S)−(E∩M∩S)=7−4=3
4. English and Science (E ∩ S): 4 students passed in both English and Science. Since 4 of these also passed Mathematics, the number of students who passed only English and Science (E ∩ S but not M) is:
(E∩S)−(E∩M∩S)=4−4=0
Step 2: Calculate Students Passing Only One Subject
1. Only English: Total students who passed English = 15. The students who passed English but not Mathematics or Science:
E−(E∩M)−(E∩S)+(E∩M∩S)=15−6−4+4=9
2. Only Mathematics: Total students who passed Mathematics = 12. The students who passed Mathematics but not English or Science:
M−(E∩M)−(M∩S)+(E∩M∩S)=12−6−7+4=3
3. Only Science: Total students who passed Science = 8. The students who passed Science but not English or Mathematics:
S−(E∩S)−(M∩S)+(E∩M∩S)=8−4−7+4=1
Step 3: Summary of Students
- Only English = 9
- Only Mathematics = 3
- Only Science = 1
- English and Mathematics but not Science = 2
- Mathematics and Science but not English = 3
- English and Science but not Mathematics = 0
- All three subjects = 4
Final Answers
(i) Students who passed in English and Mathematics but not in Science = 2
(ii) Students who passed in Mathematics and Science but not in English = 3
(iii) Students who passed in Mathematics only = 3
(iv) Students who passed in more than one subject only = 2 (E ∩ M) + 3 (M ∩ S) + 4 (E ∩ M ∩ S) = 9
- Total students = 100
- Students passed in:
- English (E) = 15
- Mathematics (M) = 12
- Science (S) = 8
- English and Mathematics (E ∩ M) = 6
- Mathematics and Science (M ∩ S) = 7
- English and Science (E ∩ S) = 4
- All three subjects (E ∩ M ∩ S) = 4
1. All three subjects (E ∩ M ∩ S): 4 students passed in all three subjects.
2. English and Mathematics (E ∩ M): 6 students passed in both English and Mathematics. Since 4 of these also passed Science, the number of students who passed only English and Mathematics (E ∩ M but not S) is:
(E∩M)−(E∩M∩S)=6−4=2
3. Mathematics and Science (M ∩ S): 7 students passed in both Mathematics and Science. Since 4 of these also passed English, the number of students who passed only Mathematics and Science (M ∩ S but not E) is:
(M∩S)−(E∩M∩S)=7−4=3
4. English and Science (E ∩ S): 4 students passed in both English and Science. Since 4 of these also passed Mathematics, the number of students who passed only English and Science (E ∩ S but not M) is:
(E∩S)−(E∩M∩S)=4−4=0
1. Only English: Total students who passed English = 15. The students who passed English but not Mathematics or Science:
E−(E∩M)−(E∩S)+(E∩M∩S)=15−6−4+4=9
2. Only Mathematics: Total students who passed Mathematics = 12. The students who passed Mathematics but not English or Science:
M−(E∩M)−(M∩S)+(E∩M∩S)=12−6−7+4=3
3. Only Science: Total students who passed Science = 8. The students who passed Science but not English or Mathematics:
S−(E∩S)−(M∩S)+(E∩M∩S)=8−4−7+4=1
- Only English = 9
- Only Mathematics = 3
- Only Science = 1
- English and Mathematics but not Science = 2
- Mathematics and Science but not English = 3
- English and Science but not Mathematics = 0
- All three subjects = 4
(i) Students who passed in English and Mathematics but not in Science = 2
(ii) Students who passed in Mathematics and Science but not in English = 3
(iii) Students who passed in Mathematics only = 3
(iv) Students who passed in more than one subject only = 2 (E ∩ M) + 3 (M ∩ S) + 4 (E ∩ M ∩ S) = 9
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Concept Application Exercise 1.28videos
SET THEORY AND REAL NUMBER SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Concept Application Exercise 1.313videos
SET THEORY AND REAL NUMBER SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Solved Exp11videos
SET THEORY AND REAL NUMBER SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
- BOOK - CENGAGE ENGLISHCHAPTER - SOLUTIONS AND PROPERTIES OF TRIANGLE EXERCISE - Comprehension Type6videos
SOLUTIONS AND PROPERTIES OF TRIANGLE
Similar Questions
Knowledge Check
- Question 1 - Select One
Raza scored 30 marks in Maths, x marks in Science and y marks in English. What is his total score in these three subjects ?
A30+x+yB30+x−yCx+y−30D30+30x+30y
Sunny scored x marks in Maths, y marks in Science and 50 marks in English. What is his total score in these three subjects?
View SolutionIn a class of 60 students, 30 students like Mathematics, 25 like Science and 15 like both. Then, the number of students who like either Mathematics or Science is
View SolutionAnjali scores 100 marks in Mathematics and x marks in Science. what is her total score in Science and Mathematics?
View SolutionSaina secure 70 marks in Science and 80 marks in Mathematics. Find
a. the ratio of Sania's marks in Science to her marks in Mathematics.
b. the ratio of Sania's marks in Mathematics to her marks is Science.View SolutionThere are five books on Mathematics and 6 books on Physics in a book shop. In how many ways can a student buy : (i) a Mathematics book and a Physics book (ii) either a Mathematics book or a Physics book?
View SolutionThe marks obtained by 10 candidates in English and Mathematics are given below:
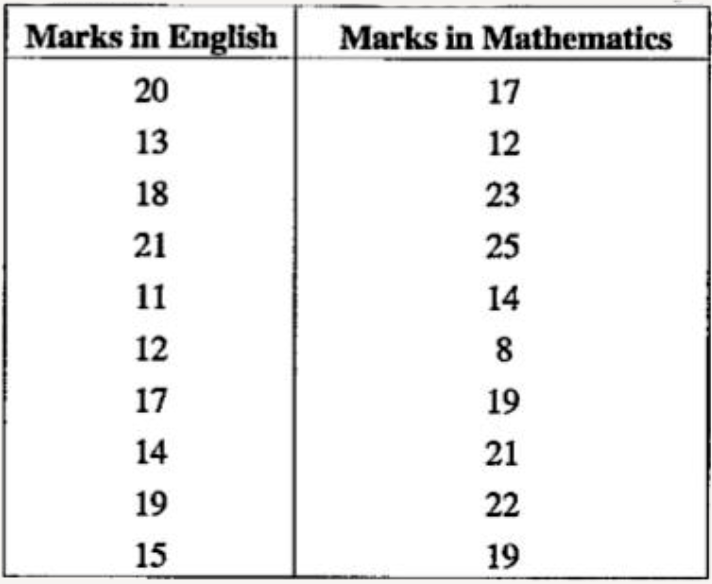
Estimate the probable score for Mathematics if the marks obtained in English are 24.View SolutionIn a class test, the sum of the marks obtained by P in Mathematics and science is 28. Had he got 3 marks more in Mathematics and 4 marks less in Science. The product of his marks, would have been 180. Find his marks in the two subjects.
View Solution

