Draw the graph of f(x)=√sinx.
Video Solution
Text Solution
We have y=f(x)=√sinx
f(x) is defined if sin≥0
Clearly, the domain of the function is x∈⋃n∈I[2nπ,π+2nπ]
Also the period of the function is 2π.
So we need to draw the graph for x∈[0,π] only.
Now 0<sinx<1 for x∈(0,π)
∴ √sinx≤sinx for x∈(0,π)
√sin0=sin0=0,√sinπ=sinπ=0 and √sinπ2=sinπ2=1
Graphs of y = sin x and y=√sinx meet at x=0,π2 and π.
For other values of x, the graph of y=√sinx lies above the graph of y = sin x.
In 3rd and 4th quadrants, y=√sinx does not exist as sinx<0 here. Thus the graph of y=√sinx is as shown in the following figure.
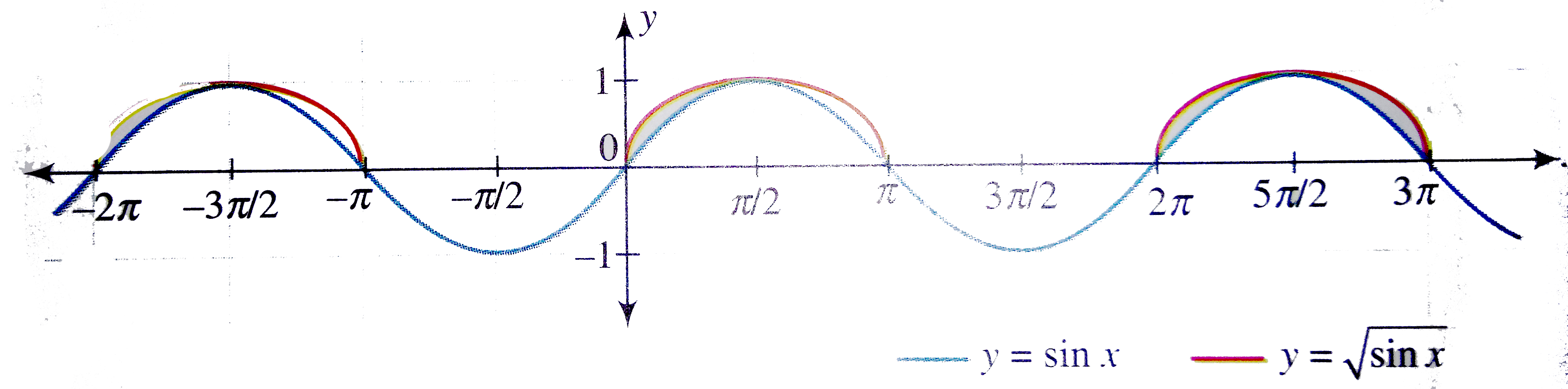
|
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGE ENGLISHCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
Similar Questions
Draw the graph of f(x)=esinx.
View SolutionDraw the graph of y=f(x)=√1−cosx
View SolutionDraw the graph of f(x)=sinx√1+tan2x−cosx√1+cot2x. Then find the range of f(x).
View SolutionDraw the graph of f(x)=x|x|.
View SolutionDraw the graph of f(x)=√1−e−x2
View SolutionDraw the graph of f(x)={sinx}, where {⋅} represents the fractional part function.
View SolutionDraw and discuss the graph of f(x)=x+√x−1
View SolutionDraw the graph of y=sinπ√x.
View SolutionDraw the graph of y=sin2x.
View SolutionDraw the graph of f(x)=sec−1(secx)
View Solution
