Question

If 0<$x_1$<$x_2$<$x_3$<$\pi$,
then prove that $\sin \left(\frac{x_1+x_2+x_3}{3}\right)<\frac{{\sin x}_1+{\sin x}_2+{\sin x}_3}{3}$
. Hence or otherwise prove that if $A,B,C$
are angles of a triangle, then the maximum value of $\sin A+\sin B+\sin C$
is $\frac{3\sqrt{3}}{2}$

Explanation

Draw the graph of y = sin x. `0 lt x lt pi` and take points `A(x_(1), sin x_(1)), B(x_(2), sin x_(2))` and `C(x_(3), sin x_(3)).`

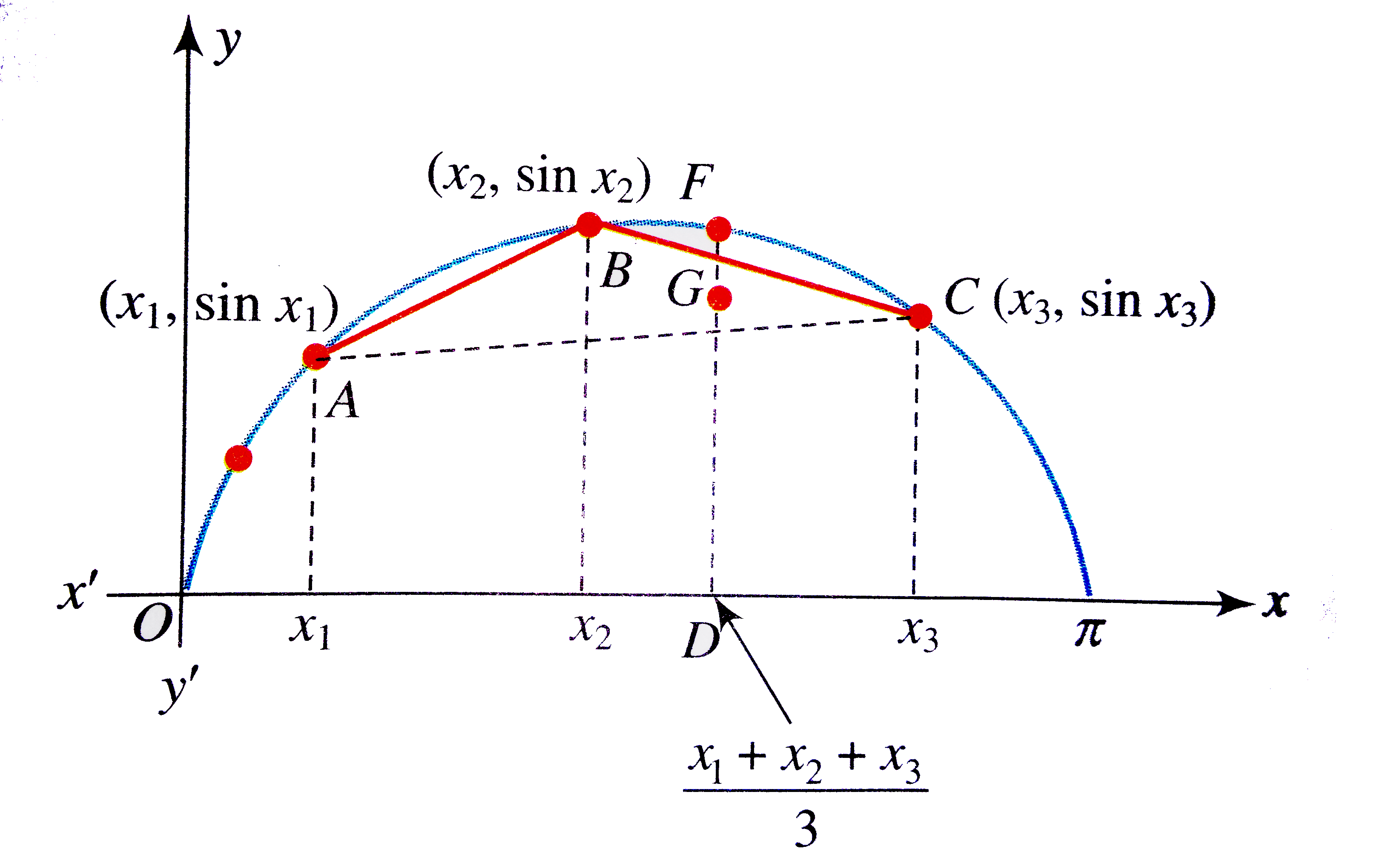
Let the points A, B, C form a traingle.
y - coordinate of the centroid G is `(sin x_(1) + sin x_(2) + sin x_(3))/(3)`
and y - coordinate of the point f is `sin ((x_(1) + x_(2) + x_(3))/(3))` (as abscissa of F is `(x_(1) + x_(2) + x_(3))/(3)`)
From the diagram, `FD gt GD`.
Hence `sin ((x_(1) + x_(2) + x_(3))/(3)) gt (sin x_(1) + sin x_(2) + sin x_(3))/(3)`
If `A + B + C = pi`, then
`sin ((A + B + C)/(3)) gt (sin A + sin B + sin C)/(3)`
`rArr` `"sin" (pi)/(3) gt (sin A + sin B + sin C)/(3)`
`rArr` `(3sqrt(3))/(2) gt sin A + sin B + sin C`
`rArr` maximum value of `(sin A + sin B + sin C) = (3sqrt(3))/(2)`