Question

A tower of height b subtends an angle at a point 0 on the ground level through the foot of the tower and at a distance a from the foot of the tower. A pole mounted on the top of the tower also subtends an equal angle at 0. The height of the pole is

Options

A. `a((a^2-b^2)/(a^2+b^2))`
B. `a((a^2+b^2)/(a^2-b^2))`
C. `b((a^2-b^2)/(a^2+b^2))`
D. `b((a^2+b^2)/(a^2-b^2))`

Answer

option 4

Explanation

Let AB be the tower abnd PB be the pole .

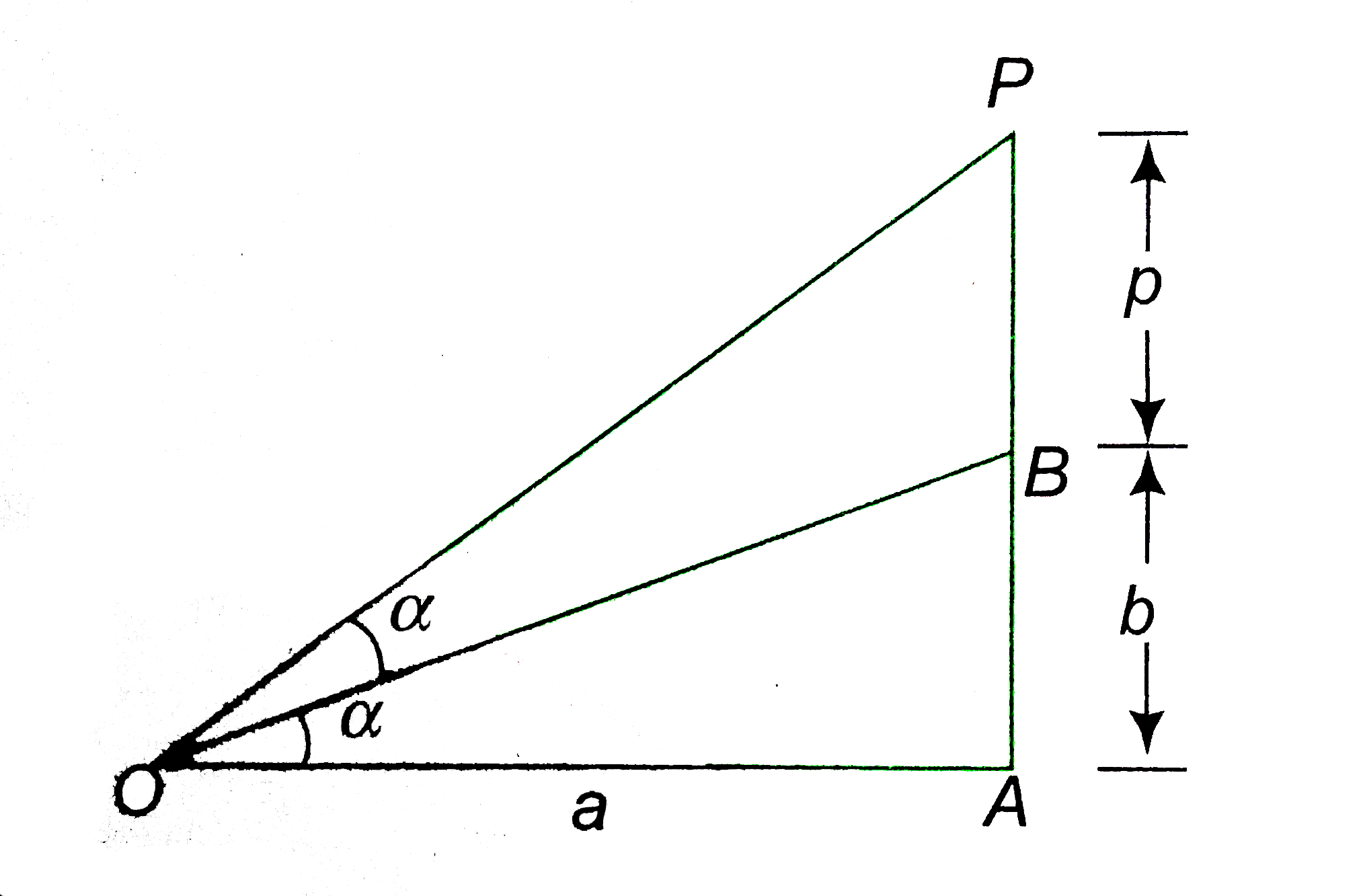
From the figure , `tan 2 alpha = (p+b)/(a)`
`therefore ( 2 tan alpha)/(1-tan^2 alpha )=(p+b)/(a)`
`rArr (2(b/a))/(1-(b/a)^2)=(p+b)/(a)`
`rArr (2ba)/(a^2-b^2)=(p+b)/a`
`rArr (2ba^2-a^2b+b^3)/(a^2+b^2)=p`
`rArr p=b ((a^2+b^2)/(a^2-b^2))`