For what real values of a do the roots of the equation x2−2x−(a2−1)=0 lie between the roots of the equation x2−2(a+1)x+a(a−1)=0.
x2−2x−(a2−1)=0 (i)
x2−2(a+1)x+a(a−1)=0 (ii)
For equation (i), x=2±√4+4(a2+1)2=1±a
Now roots of (i) lies between the roots of equation (ii).
f1(x)=x2−2x−(a2−1)
f2(x)=x2−2(a+1)x+a(a−1)
Hence the graphs of expressions for the equation are as shown in the following figure :
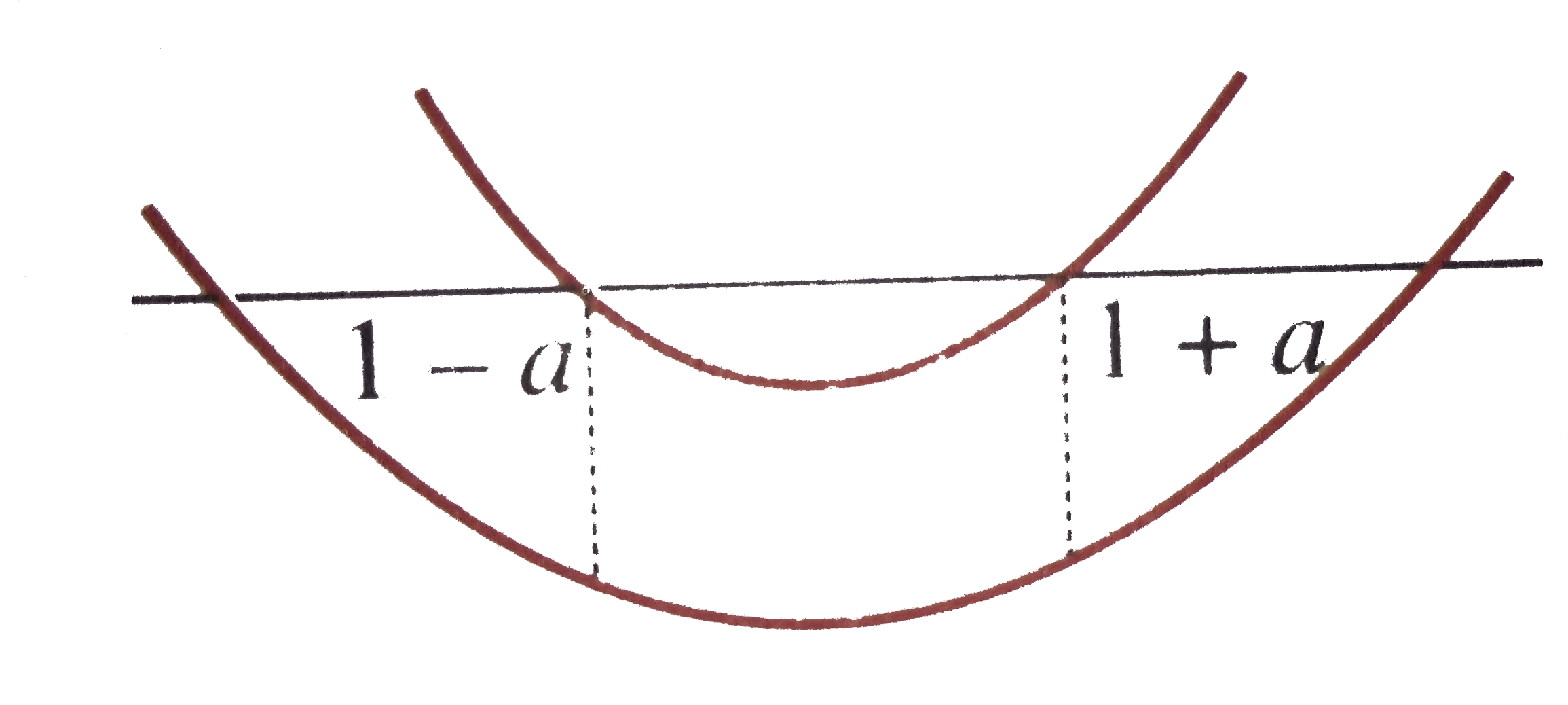
If the roots f1(x)=0 are real.
D≥0
⇒ 4+4(a2−1)≥0
⇒ a2≥0, which is always true
Also f2(1−a)<0andf2(1+a)<0
⇒ (1−a2)−2(a+1)(1−a)+a(a−1)<0
⇒ (1−a)[(1−a)−2a−2−a]<0
⇒ (1−a)(−4a−1)<0
⇒ (a−1)(4a+1)<0
⇒ −14<a<1 (iii)
and (1+a)2−2(a+1)(a+1)+a(a−1)<0
⇒ −(a+1)2+a(a−1)<0
⇒ −a2−2a−1+a2−a<0
⇒ 3a+1>0
⇒ a>−13 (iv)
From (iii) and (iv), common values
−14<a<1
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
17 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
Similar Questions
If the range of the values of a for which the roots of the equation x2−2x−a2+1=0 lie between the roots of the equation x2−2(a+1)x+a(a−1)=0 is (p,q), then find the value of (q−1p).
View SolutionIf the range of the values of a for which the roots of the equation x2−2x−a2+1=0 lie between the roots of the equation x2−2(a+1)x+a(a−1)=0 is (p,q), then find the value of (q−1p).
View Solution
Knowledge Check
The roots of the quadratic equation x2+2x+1=0 are:
AReal and distinctBReal and equalCDistinctDNot real/imaginary
For what real values of k both the roots of equation x2+2(k−3)x+9=−0 lie between -6 and 1.
View SolutionFind the roots of the equation 2x2−x+18=0
View SolutionSet of values of 'a' for which both roots of the equation x2−2x−a2=0 lie between the roots of the equation x2−2x+a2−11a+12=0, is
View SolutionFind the smallest positive integral value of a for which the greater root of the equation x2−(a2+a+1)x+a(a2+1)=0 lies between the roots of the equation x2−a2x−2(a2−2)=0
View SolutionThe roots of the equation 12x2+x−1=0 is :
View SolutionIf both roots of the equation x2−2ax+a2−1=0 lie between (−2,2) then a lies in the interval
View SolutionIf one root of the equation ix2−2(1+i)x+(2−i)=0 is 2- I then the root is
View Solution
