If 2≤|x|≤5, then find the values of x from the graph of y=|x|.
To solve the problem, we need to find the values of x such that 2≤|x|≤5 using the graph of the function y=|x|.
1. Understanding the Absolute Value Inequality:
The inequality 2≤|x|≤5 can be broken down into two parts:
- |x|≥2
- |x|≤5
2. Graph of y=|x|:
The graph of y=|x| is a V-shaped graph that opens upwards. It intersects the y-axis at the origin (0,0) and has points at (2,2), (-2,2), (5,5), and (-5,5).
3. Finding the Range for |x|≤5:
The condition |x|≤5 implies that:
−5≤x≤5
This means x can take any value between -5 and 5, inclusive.
4. Finding the Range for |x|≥2:
The condition |x|≥2 implies that:
x≤−2orx≥2
This means x can take values less than or equal to -2 or greater than or equal to 2.
5. Combining the Inequalities:
Now, we need to find the intersection of the two ranges:
- From |x|≤5: −5≤x≤5
- From |x|≥2: x≤−2 or x≥2
Therefore, we can express the valid intervals for x:
- For x≤−2: The intersection with −5≤x≤5 gives us −5≤x≤−2.
- For x≥2: The intersection with −5≤x≤5 gives us 2≤x≤5.
6. Final Result:
Combining these intervals, we find:
x∈(−5,−2)∪(2,5)
Conclusion:
The values of x that satisfy the inequality 2≤|x|≤5 are:
x∈(−5,−2)∪(2,5)
The inequality 2≤|x|≤5 can be broken down into two parts:
- |x|≥2
- |x|≤5
The graph of y=|x| is a V-shaped graph that opens upwards. It intersects the y-axis at the origin (0,0) and has points at (2,2), (-2,2), (5,5), and (-5,5).
The condition |x|≤5 implies that:
−5≤x≤5
This means x can take any value between -5 and 5, inclusive.
The condition |x|≥2 implies that:
x≤−2orx≥2
This means x can take values less than or equal to -2 or greater than or equal to 2.
Now, we need to find the intersection of the two ranges:
- From |x|≤5: −5≤x≤5
- From |x|≥2: x≤−2 or x≥2
- For x≤−2: The intersection with −5≤x≤5 gives us −5≤x≤−2.
- For x≥2: The intersection with −5≤x≤5 gives us 2≤x≤5.
Combining these intervals, we find:
x∈(−5,−2)∪(2,5)
The values of x that satisfy the inequality 2≤|x|≤5 are:
x∈(−5,−2)∪(2,5)
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGE ENGLISHChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:EXERCISES
Explore 34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBook:CENGAGE ENGLISHChapter:GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSExercise:Exercises
Explore 17 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBook:CENGAGE ENGLISHChapter:GRAPHS OF TRIGONOMETRIC FUNCTIONSExercise:Exercises
Explore 22 Videos
Similar Questions
Knowledge Check
If 0≤t≤1, which of the following graphs is the graph of y versus x where x and y are related by the parametric equations y=t2 and x=√t ?
A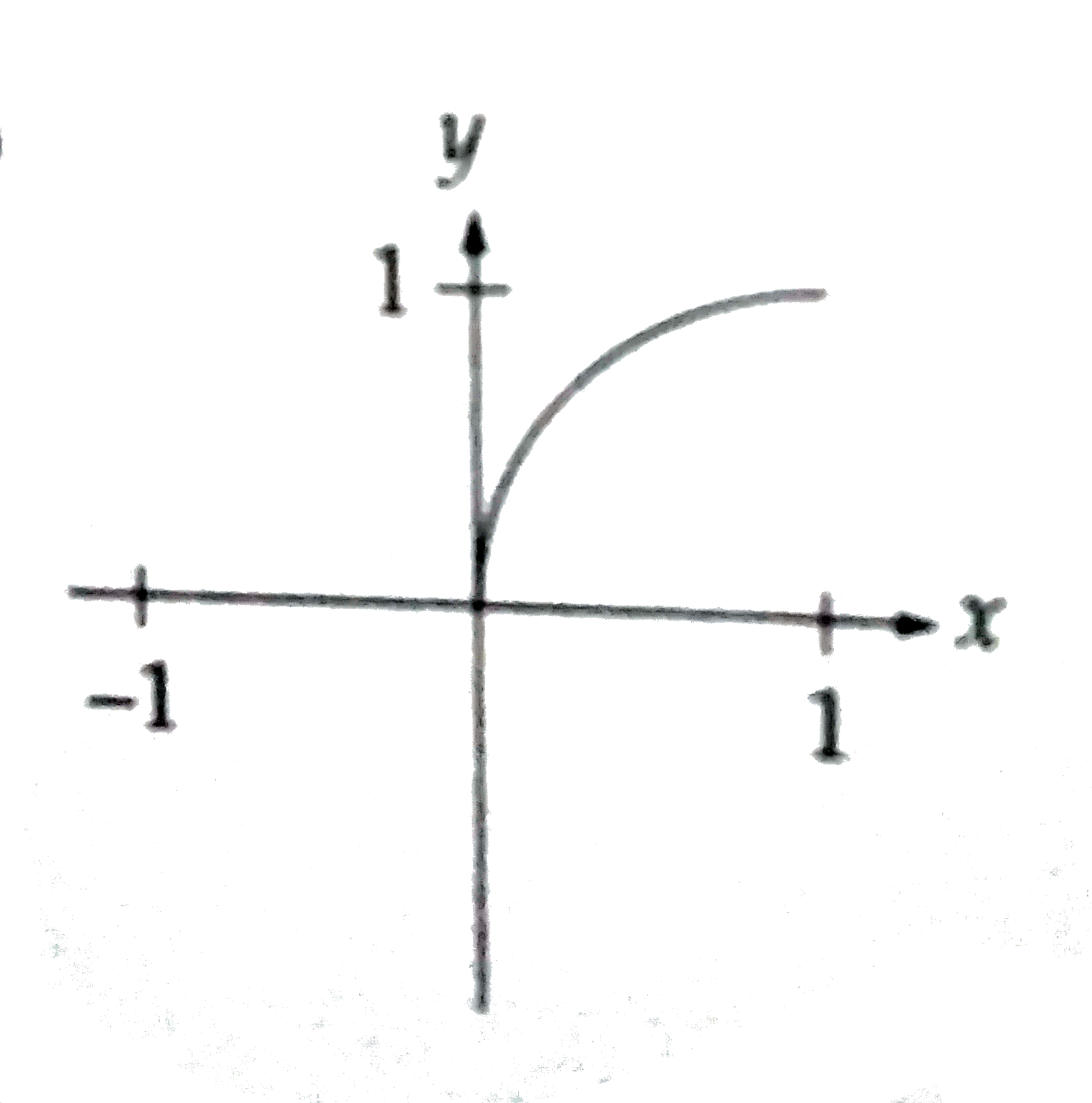 B
B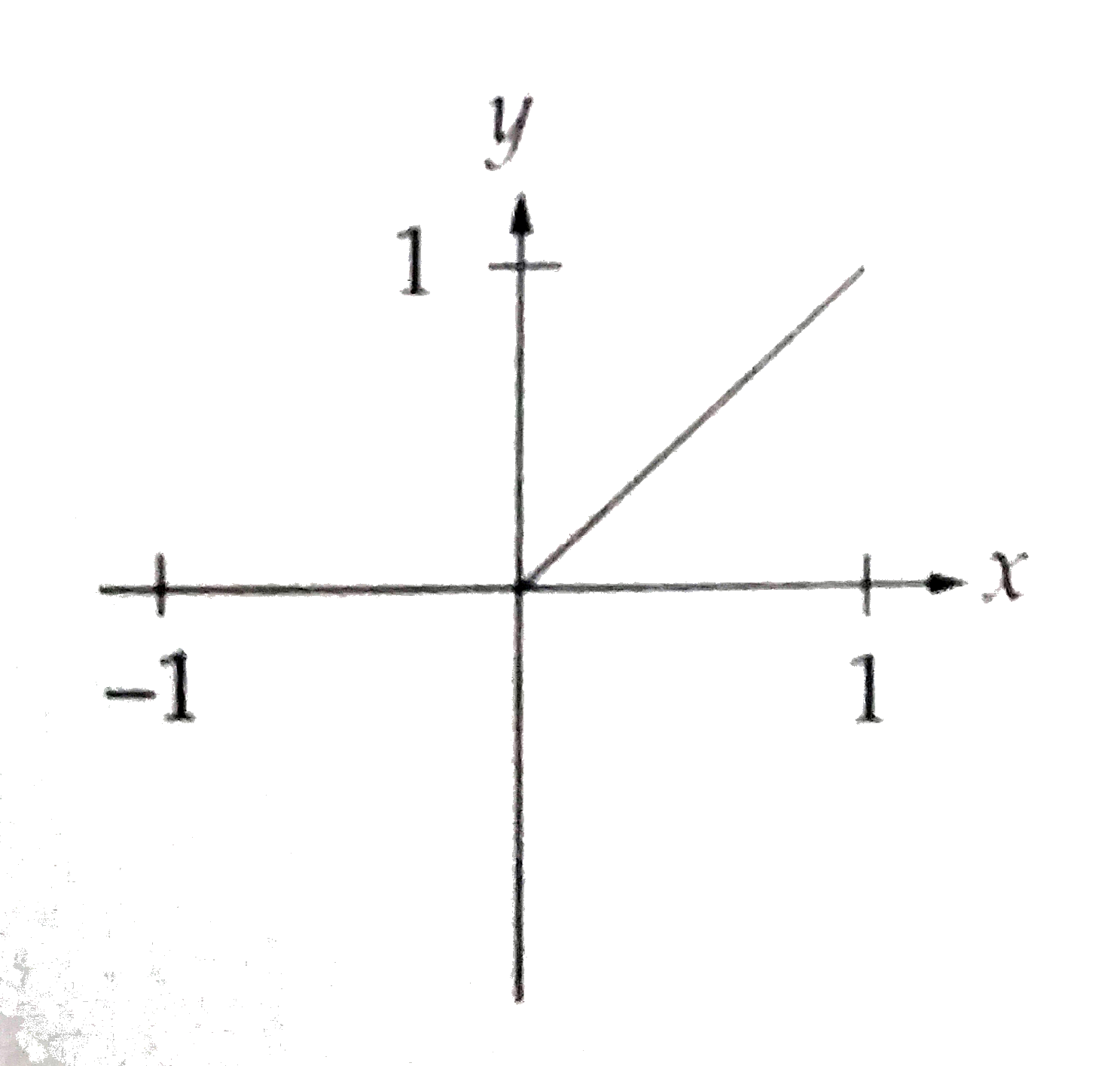 C
C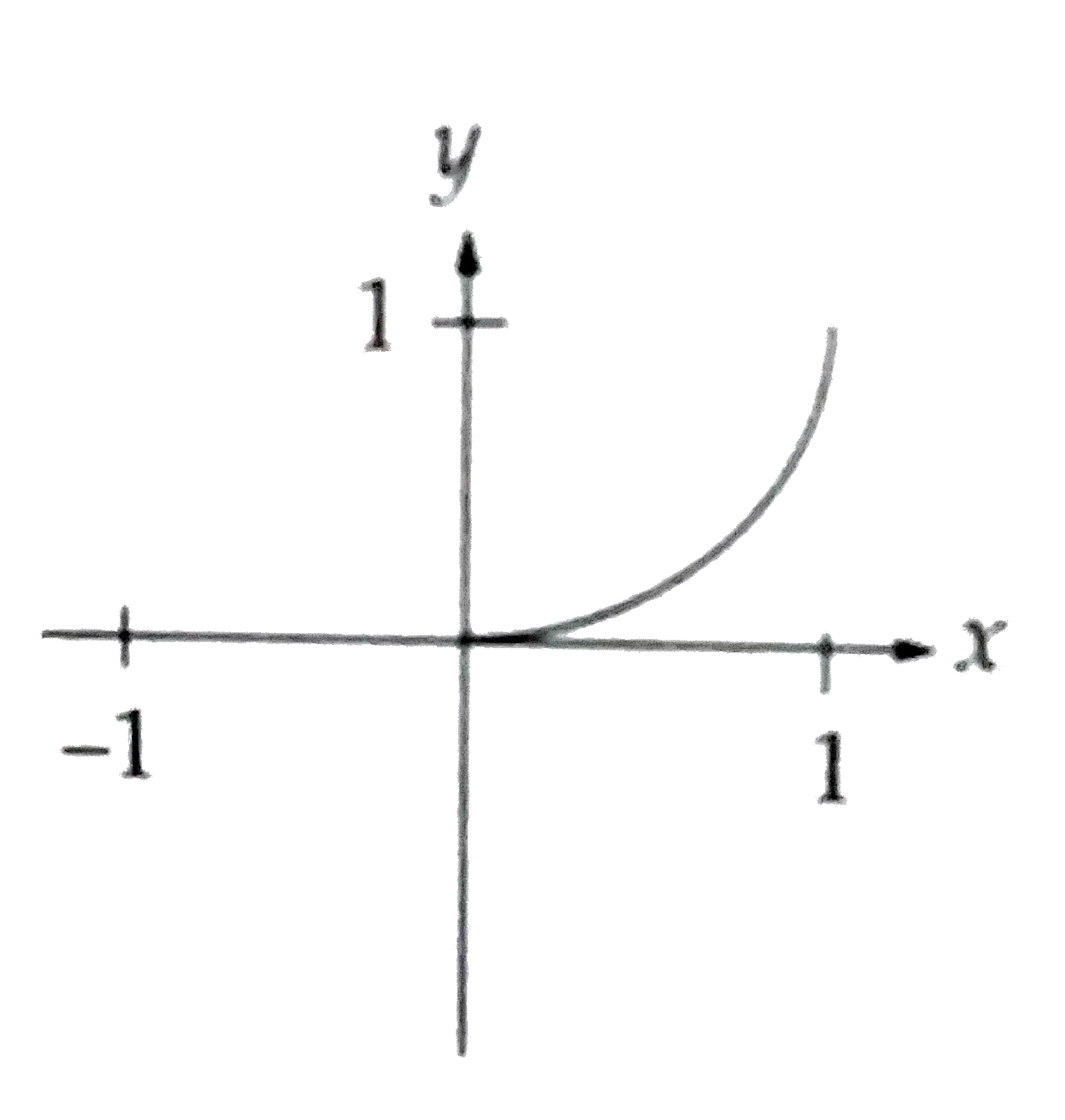 D
D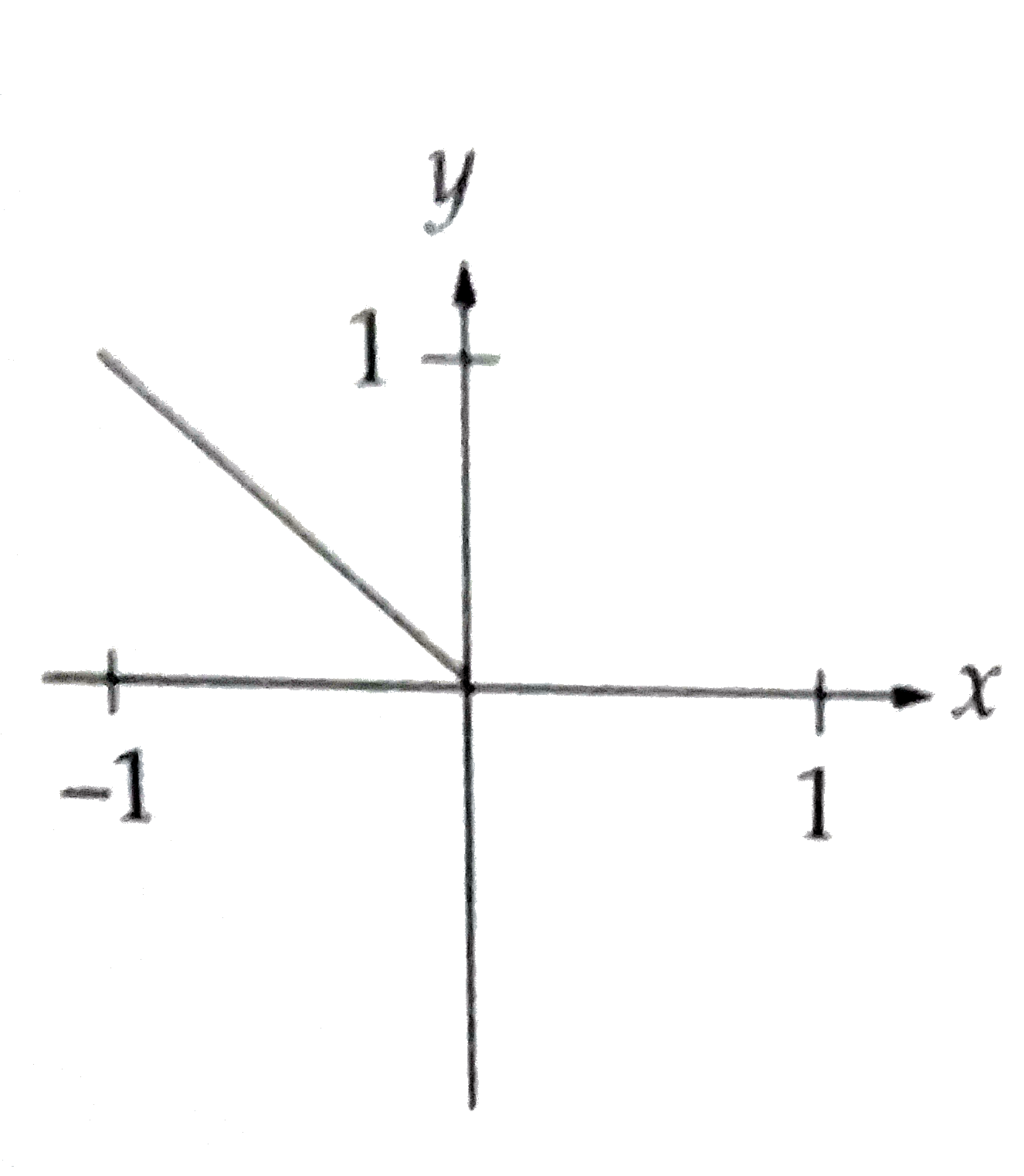
If 02≤x≤2, the maximum value of f(x)=1−x2 is
A2B1C0D−1If |x|≤2and|y|≤1, then what is the least possible value of x-y?
A−3B−2C−1D0
If x+siny=2014 and x+2014cosy=2013,0≤y≤π2 , then find the value of [x+y]−2005
(where [.] denotes greatest integer function)
View SolutionFor 2<x<4 find the values of |x|.
(ii) For −3≤x≤−1, find the values of |x|.
(iii) For −3≤x<1, find the values of |x|
(iv) For −5<x<7 find the values of |x-2|
(v) For 1≤x≤5 find fthe values of |2x -7|
View SolutionUse real number line to find the range of values of x for which :
−1<x≤6and−2≤x≤3.
View SolutionIf −2≤3x−7≤8, find x.
View SolutionIf cosx=√1−sin2x,0≤x≤π then a value of x is
View Solution