If a continuous function f defined on the real line R assume positive and negative values in R, then the equation f(x)=0 has a root in R. For example, if it is known that a continuous function f on R is positive at some point and its minimum value is negative, then the equation f(x)=0 has a root in R. Consider f(x)=kex−x, for all real x where k is a real constant.
For k > 0, the set of all values of k for which y=kex−x=0has two distinct roots is
a. 1e
b. 1
c. e
d. loge2
(a) kex−x=0 to have only one positive root means the line y=xk must be tangential to the curve y=ex.
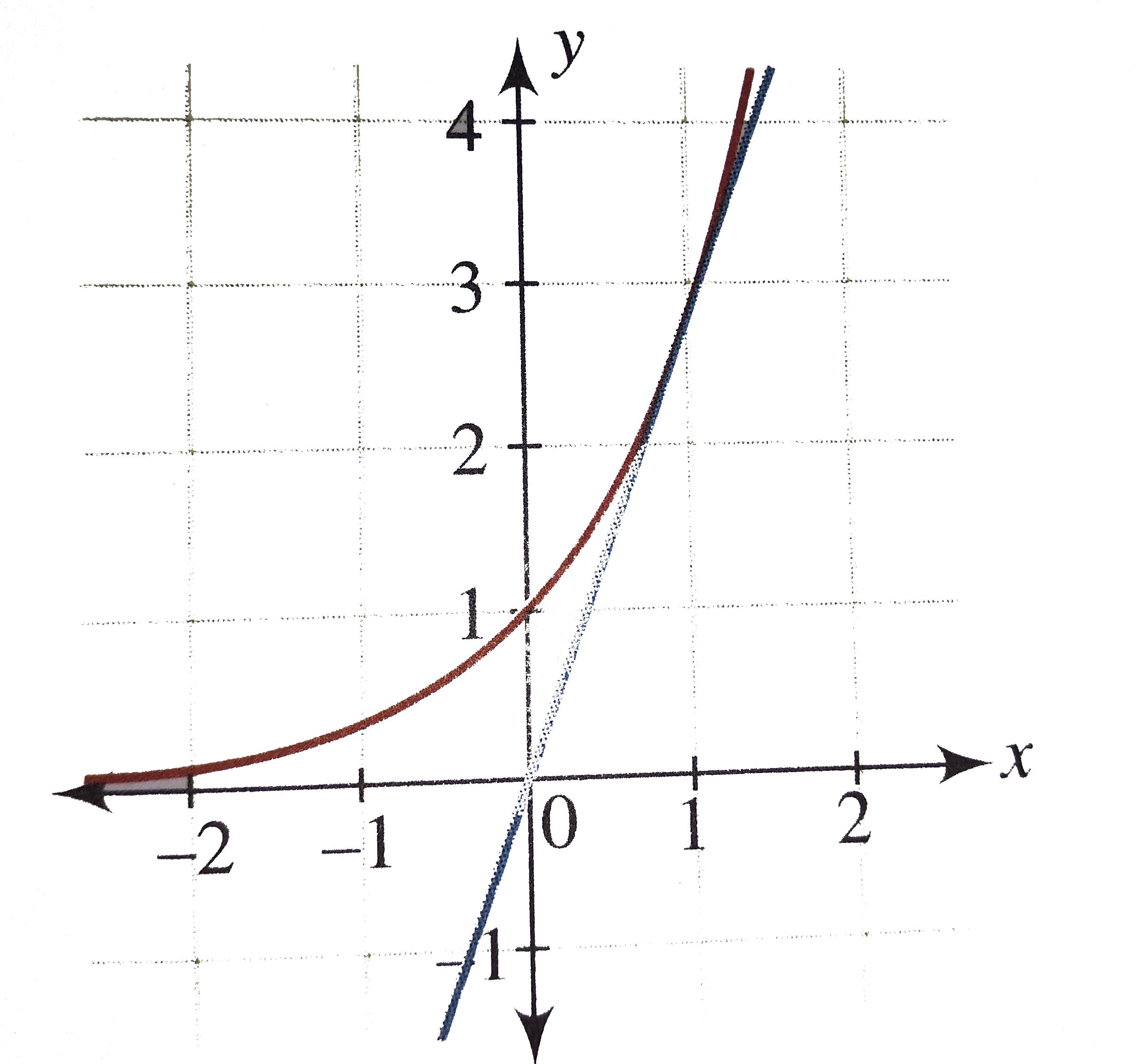
Let the line touch the curve at (x1,y1), then
(dydx)x1=ex1=1k
Also y1=ex1andy1=x−1k
⇒x1=1⇒k=1/e
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
17 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
Similar Questions
If a continuous function f defined on the real line R assume positive and negative values in R, then the equation f(x)=0 has a root in R. For example, if it is known that a continuous function f on R is positive at some point and its minimum value is negative, then the equation f(x)=0 has a root in R. Consider f(x)=kex−x, for all real x where k is a real constant.
The positive value of k for which kex−x=0 has only one root is
View SolutionLet f(x) be a continuous function defined for ∀x∈R , if f(x) take rational values ∀x∈Randf(2)=198, then f(22) = ……
View SolutionIf f(x)>x;∀x∈R. Then the equation f(f(x))−x=0, has
View Solutionconsider the function f(X) =x+cosx -a
values of a for which f(X) =0 has exactly one negative root are
View Solutionconsider the function f(X) =x+cosx -a
values of a which f(X) =0 has exactly one positive root are
View SolutionIf f(x) is a continuous function such that its value ∀x∈R is a rational number and f(1)+f(2)=6, then the value of f(3) is equal to
View SolutionIf a real valued function f(x) satisfies the equation f(x+y)=f(x)+f(y) for all x,y∈R then f(x) is
View SolutionIf f be a function defined as f(x) = p for each x∈R, where p is a real number, then f is called
View SolutionA function f:R→R is defined as f(x)=4x−1,x∈R, then prove that f is one - one.
View SolutionA real valued function f(x) satisfies the functional equation f(x−y)=f(x)f(y)−f(a−x)f(a+y), where a is a given constant and f(0)=1 , f(2a-x) =?
View Solution
