If f(x)=3x2+ax+a+1x2+x−2, then which of the following can be correct (a) (lim)x→1f(x)fora=−2 (b) (lim)x→−2f(x)fora=13 (c) (lim)x→1f(x)=43 (d) (lim)x→−2f(x)=−13
ln a1
ean
a_(1)
an
The correct Answer is:A, B, C, D
To solve the problem, we need to evaluate the limit of the function f(x)=3x2+ax+(a+1)x2+x−2 for different values of a and at specific points.
1. Identify the function and the limits to evaluate:
The function is given as:
f(x)=3x2+ax+(a+1)x2+x−2
We need to evaluate the limits for the following conditions:
- (a) limx→1f(x) for a=−2
- (b) limx→−2f(x) for a=13
- (c) limx→1f(x)=43
- (d) limx→−2f(x)=−13
2. Evaluate limit (a): limx→1f(x) for a=−2
- Substitute x=1:
f(1)=3(1)2+(−2)(1)+(−2+1)(1)2+(1)−2=3−2−11+1−2=00
- Since we have a 0/0 form, we apply L'Hôpital's Rule:
- Differentiate the numerator and denominator:
Numerator: ddx(3x2−2x−1)=6x−2
Denominator: ddx(x2+x−2)=2x+1
- Now, applying L'Hôpital's Rule:
limx→1f(x)=limx→16x−22x+1=6(1)−22(1)+1=43
- Since a=−2 gives us 43, option (a) is correct.
3. Evaluate limit (b): limx→−2f(x) for a=13
- Substitute x=−2:
f(−2)=3(−2)2+13(−2)+(13+1)(−2)2+(−2)−2=12−26+144−2−2=00
- Again, we apply L'Hôpital's Rule:
- Differentiate the numerator and denominator:
Numerator: ddx(3x2+13x+14)=6x+13
Denominator: ddx(x2+x−2)=2x+1
- Now, applying L'Hôpital's Rule:
limx→−2f(x)=limx→−26x+132x+1=6(−2)+132(−2)+1=−12+13−4+1=1−3=−13
- Since a=13 gives us −13, option (b) is correct.
4. Evaluate limit (c): limx→1f(x)=43
- From the previous calculation, we already found that:
limx→1f(x)=43
- Therefore, option (c) is correct.
5. Evaluate limit (d): limx→−2f(x)=−13
- From the previous calculation, we found that:
limx→−2f(x)=−13
- Therefore, option (d) is also correct.
Conclusion
All options (a), (b), (c), and (d) are correct.
The function is given as:
f(x)=3x2+ax+(a+1)x2+x−2
We need to evaluate the limits for the following conditions:
- (a) limx→1f(x) for a=−2
- (b) limx→−2f(x) for a=13
- (c) limx→1f(x)=43
- (d) limx→−2f(x)=−13
- Substitute x=1:
f(1)=3(1)2+(−2)(1)+(−2+1)(1)2+(1)−2=3−2−11+1−2=00
- Since we have a 0/0 form, we apply L'Hôpital's Rule:
- Differentiate the numerator and denominator:
Numerator: ddx(3x2−2x−1)=6x−2
Denominator: ddx(x2+x−2)=2x+1
- Now, applying L'Hôpital's Rule:
limx→1f(x)=limx→16x−22x+1=6(1)−22(1)+1=43
- Since a=−2 gives us 43, option (a) is correct.
- Substitute x=−2:
f(−2)=3(−2)2+13(−2)+(13+1)(−2)2+(−2)−2=12−26+144−2−2=00
- Again, we apply L'Hôpital's Rule:
- Differentiate the numerator and denominator:
Numerator: ddx(3x2+13x+14)=6x+13
Denominator: ddx(x2+x−2)=2x+1
- Now, applying L'Hôpital's Rule:
limx→−2f(x)=limx→−26x+132x+1=6(−2)+132(−2)+1=−12+13−4+1=1−3=−13
- Since a=13 gives us −13, option (b) is correct.
- From the previous calculation, we already found that:
limx→1f(x)=43
- Therefore, option (c) is correct.
- From the previous calculation, we found that:
limx→−2f(x)=−13
- Therefore, option (d) is also correct.
All options (a), (b), (c), and (d) are correct.
Topper's Solved these Questions
- LIMITSBOOK - CENGAGE ENGLISHCHAPTER - LIMITSEXERCISE - Linked Comprehension Type
20 Videos
- LIMITSBOOK - CENGAGE ENGLISHCHAPTER - LIMITSEXERCISE - Matrix Match Type
5 Videos
- LIMITSBOOK - CENGAGE ENGLISHCHAPTER - LIMITSEXERCISE - Exercises (Single Correct Answer Type)
76 Videos
- JEE 2019BOOK - CENGAGE ENGLISHCHAPTER - JEE 2019EXERCISE - Chapter 10
9 Videos
- LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSBOOK - CENGAGE ENGLISHCHAPTER - LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSEXERCISE - DPP 1.2
10 Videos
Similar Questions
If f(x)=3x2+ax+a+1x2+x−2, then which of the following can be correct (lim)x→1f(x)eξstsa=−2 (lim)x→−2f(x)eξstsa=13 (lim)x→1f(x)=43 (lim)x→−2f(x)=−13
View SolutionWhich of the following limits tends to unity? (a)(lim)x→0sin(tanx)sinx (b) (lim)x→π2sin(cosx)cosx (c) (lim)x→0sinex−1x (d) (lim)x→0√1+x−√1−xx
View SolutionConsider the following graph of the function y=f(x). Which of the following is/are correct? fig. 1. (lim)x→1f(x) does not exist. 2.(lim)x→2f(x) does not exist. 3. (lim)x→3f(x)=3. 4. (lim)x−−→1.99f(x)= exists
View SolutionWhich of the following is and determinate form (lim)x→1x3−1x−1 b. (lim)x→0(1+x)1/x c. (lim)x→1(1x2−1−1x−1) d. (lim)x→0(|x|)s∈R
View Solution(lim)x→1(1−x)tan(πx)2=___
View SolutionGiven (lim)x→0f(x)x2=2,where [.] denotes the greatest integer function, then (A) (lim)x→0[f(x)]=0 (B) (lim)x→0[f(x)]=1 (C)(lim)x→0[f(x)x] does not exist (D)(lim)x→0[f(x)x] exists
View SolutionIf f(x)=x(e|x|+[x]−2|x|+[x]) then (where [.] represents the greatest integer function) (lim)x→0+f(x)=−1 b. (lim)x→0−f(x)=0 c. (lim)x→0□f(x)=−1 d. (lim)x→0□f(x)=0
View SolutionEvaluate: (lim)x→2x−2(log)a(x−1)
View SolutionGiven a real-valued function f such that f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩tan2{x}(x2−[x]2)√{x}cot{x},forx<0,fx>0 Where [x] is the integral part and {x} is the fractional part of x, then (lim)x→0+f(x)=1 , (lim)x→0−f(x)=cot1, cot−1((lim)x→0−f(x))2=1, tan−1((lim)x→0+f(x))=π4
View SolutionConsider the following graph of the function y=f(x). Which of the following is//are correct?
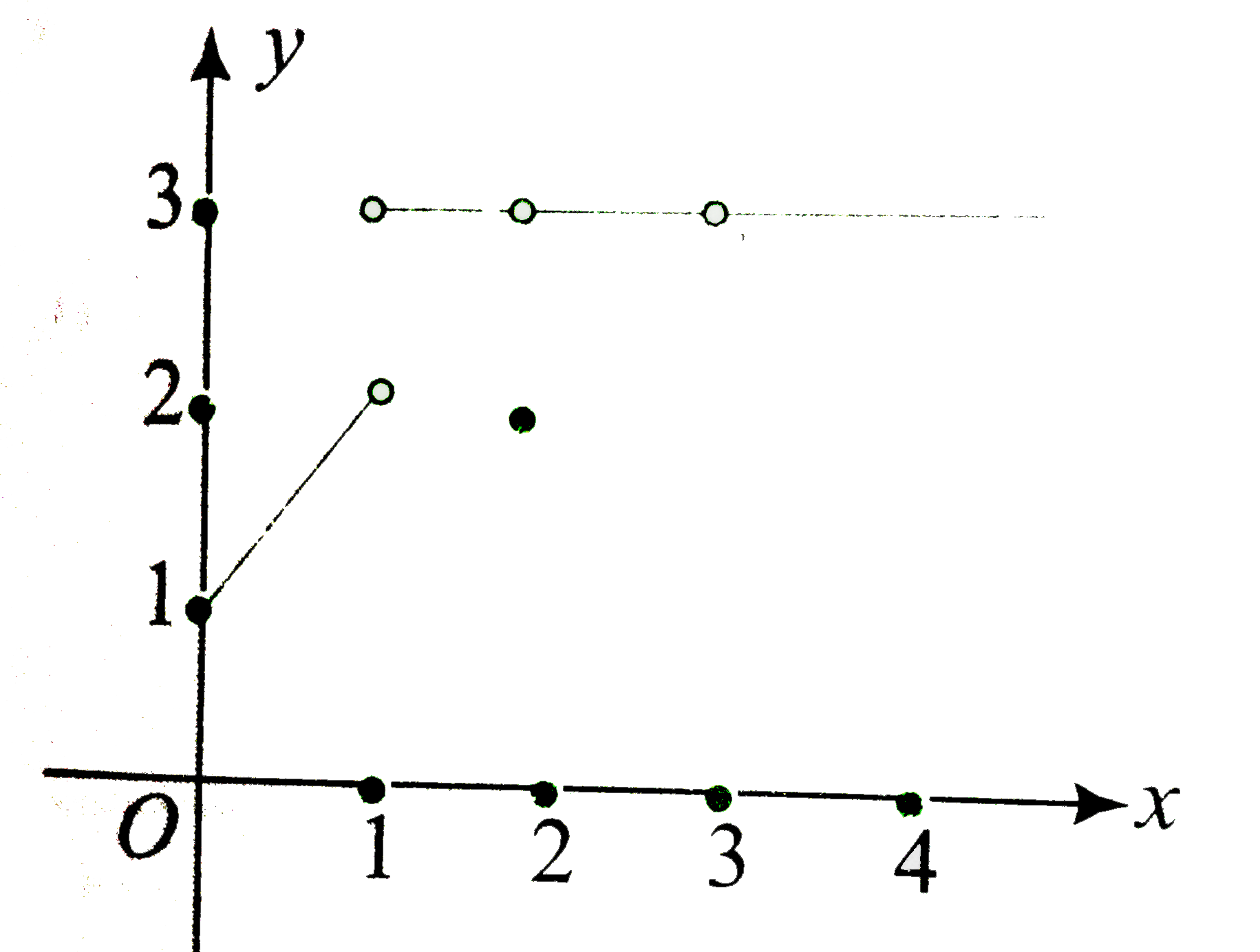
(a)limx→1f(x) does not exist.
(b)limx→2f(x) does not exist.
(c)limx→3f(x)=3.
(d)limx→1.99f(x)exists.
View Solution
