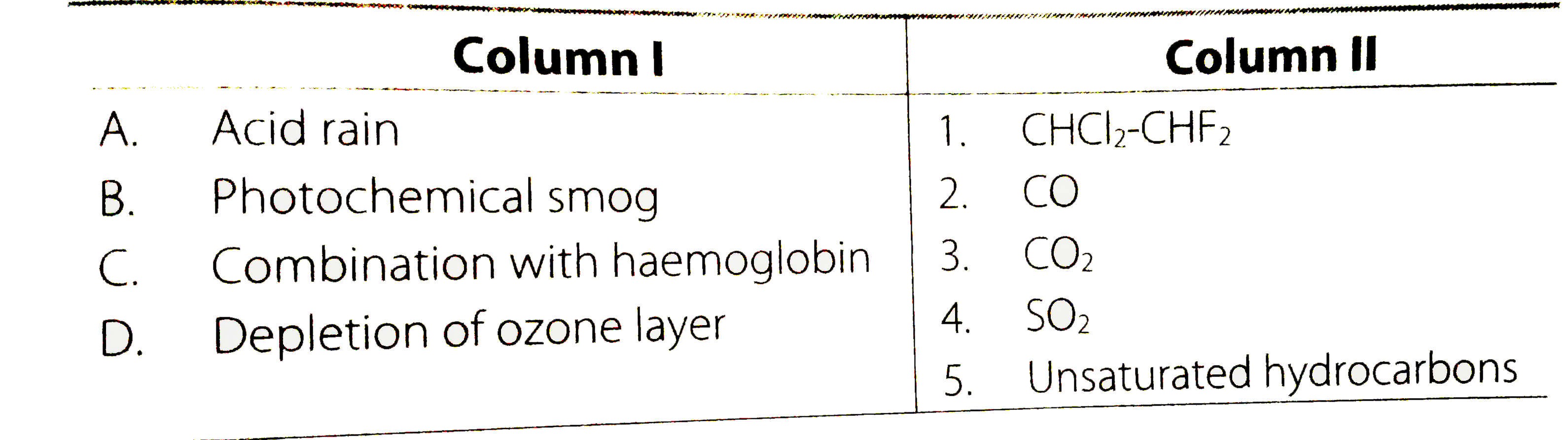
Match the terms given in Column I with the compound given in Column II.
The correct Answer is:4
a. Let f(x)=ax2+bx(∵f(0)=0)
Given ∫10f(x)dx=1
=2a+3b=6
=(a,b)=(0,2) and (3,0)
b. f(x)=sin(x2)+cos(x2)
=√2cos(x2−π4)
For maximum value x2−π4=2nπ,nεZ
⇒x2=2nπ+π4,nεZ
⇒x=±√x4±√9π4 as xε[−√13,√13]
c. I=∫2−23x2(1+ex)dx...............1
=∫2−23(−x)21+e−xdx
∴I=∫2−2ex(3x)2ex+1dx............2
Addding 1 and 2
⇒I+I=∫2−23x2(1+ex)dx+∫2−2ex(3x2)ex+1dx
=∫2−23x2dx=2∫203x2dx=16
⇒I=8
d. We have I=∫1/21/2cos2x.log(1+x1−x)dx∫1/20cos2x.log(1+x1−x)dx
Let f(x)=cos2xI(1+x1−x)
∴f(−x)=cos(−2x)In(1−x1+x)
=−cos(2x)In(1+x1−x)=−f(x)
Thus, f(x) is an odd function.
⇒I=0
Topper's Solved these Questions
Similar Questions
Match the terms given in Column I with the items given in Column II. (One to one match only)
 View Solution
View SolutionMatch the terms given in column I with the units given in column II.
 View Solution
View SolutionMatch the terms given in Column-I with their descriptions given in Column-II and select the correct option from the codes given below.
 View Solution
View SolutionMatch the property given in Column I with the element given in Column II.
 View Solution
View SolutionMatch the reactions given in Column I with the names given in Column II.
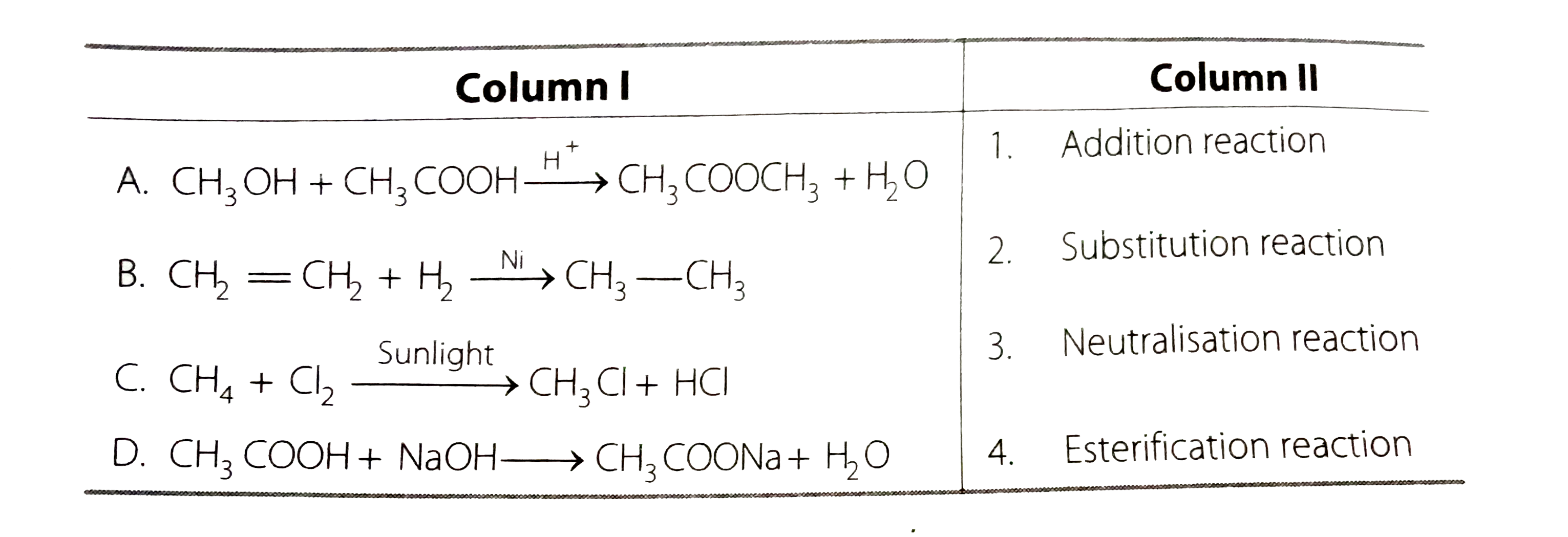 View Solution
View Solutionmatch the items given in column I with the items given in column II.
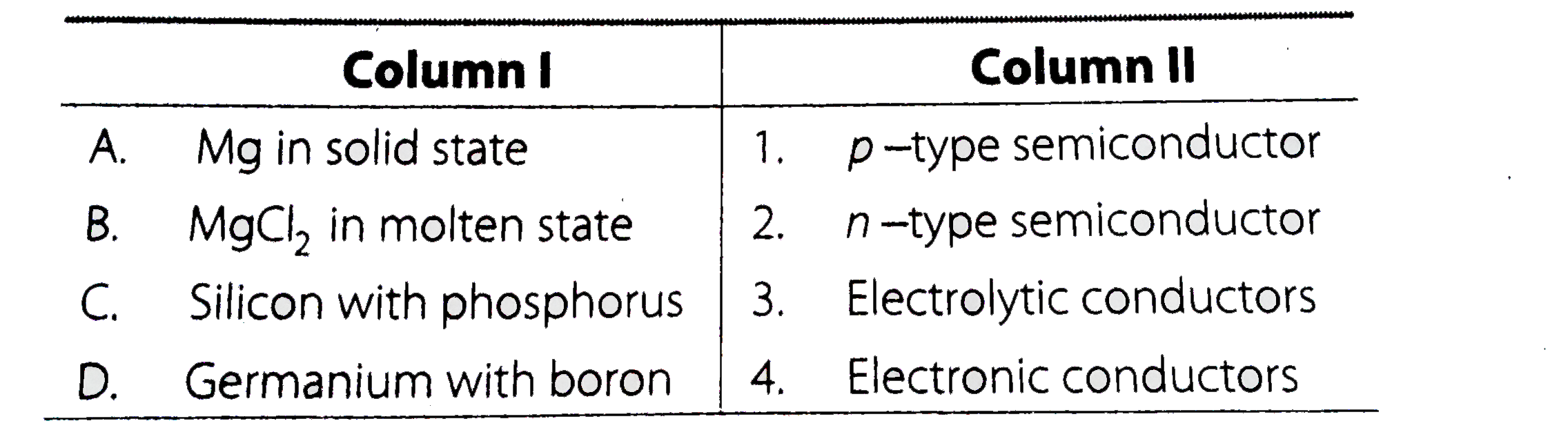 View Solution
View Solutionmatch the items given in column I with the items given in column II.
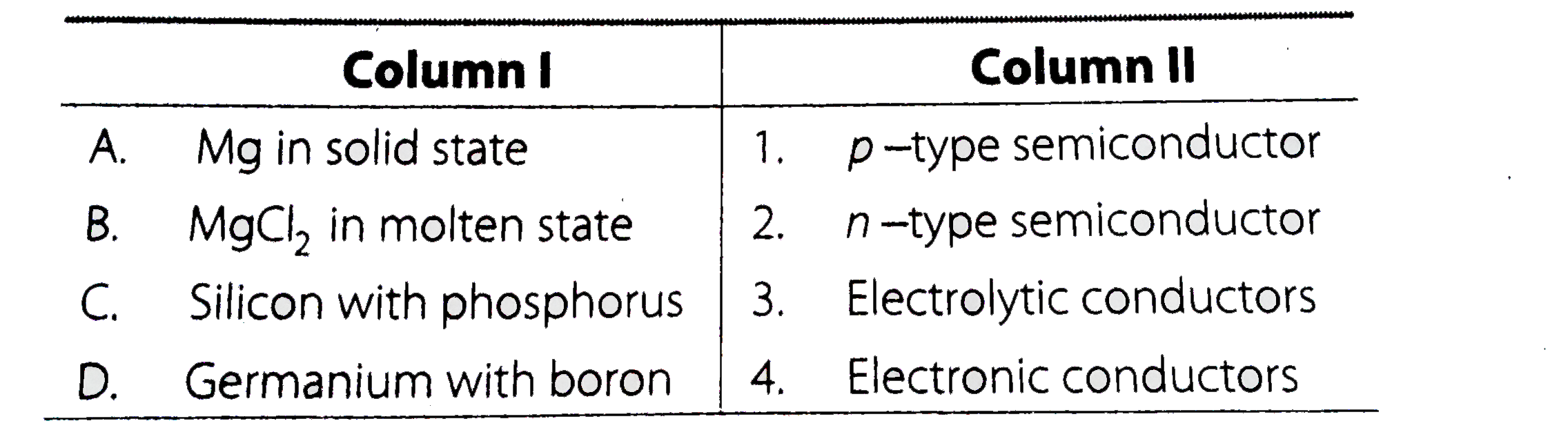 View Solution
View SolutionMatch the reactions given in Column I with the names givn in Column II.
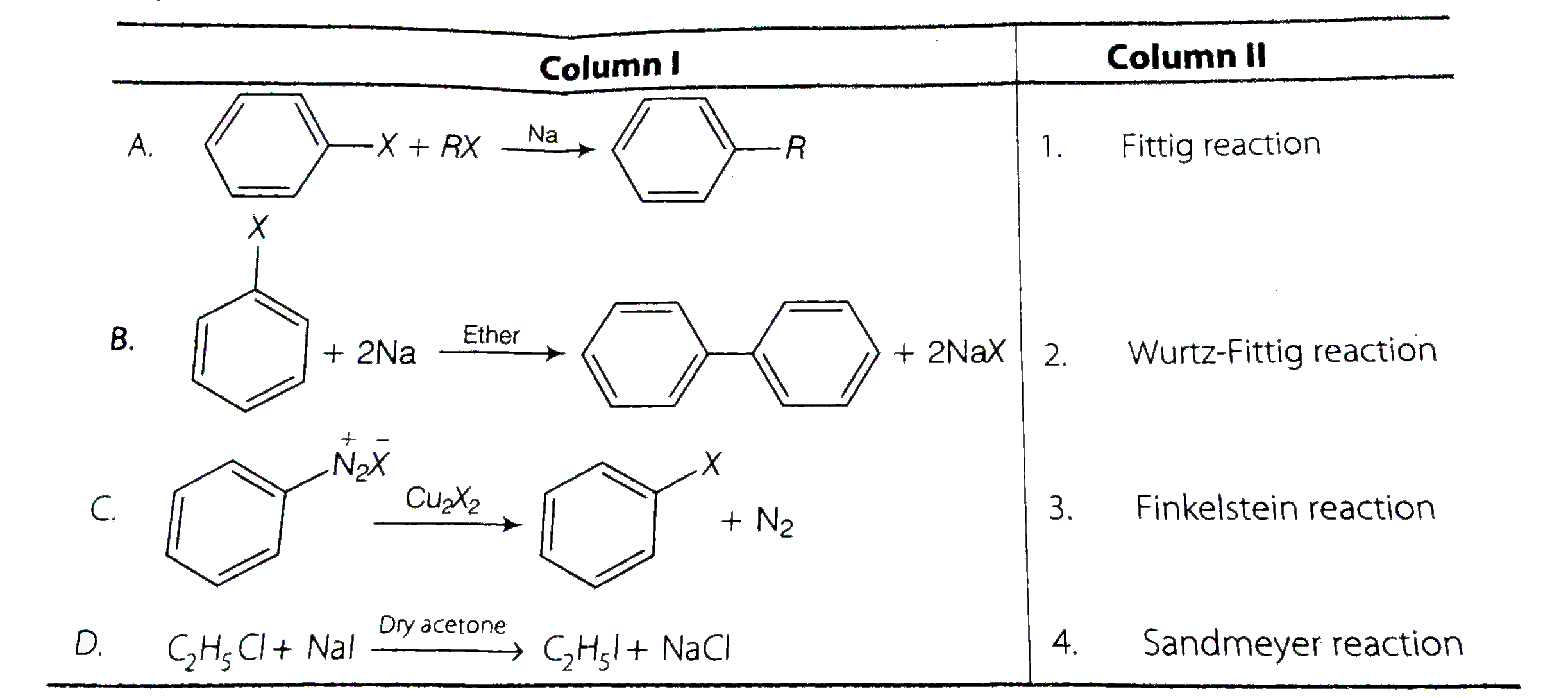 View Solution
View SolutionMatch the properties given in Column I with the metals given in Column II
 View Solution
View SolutionMatch the properties given in Column I with the metals given in Column II.
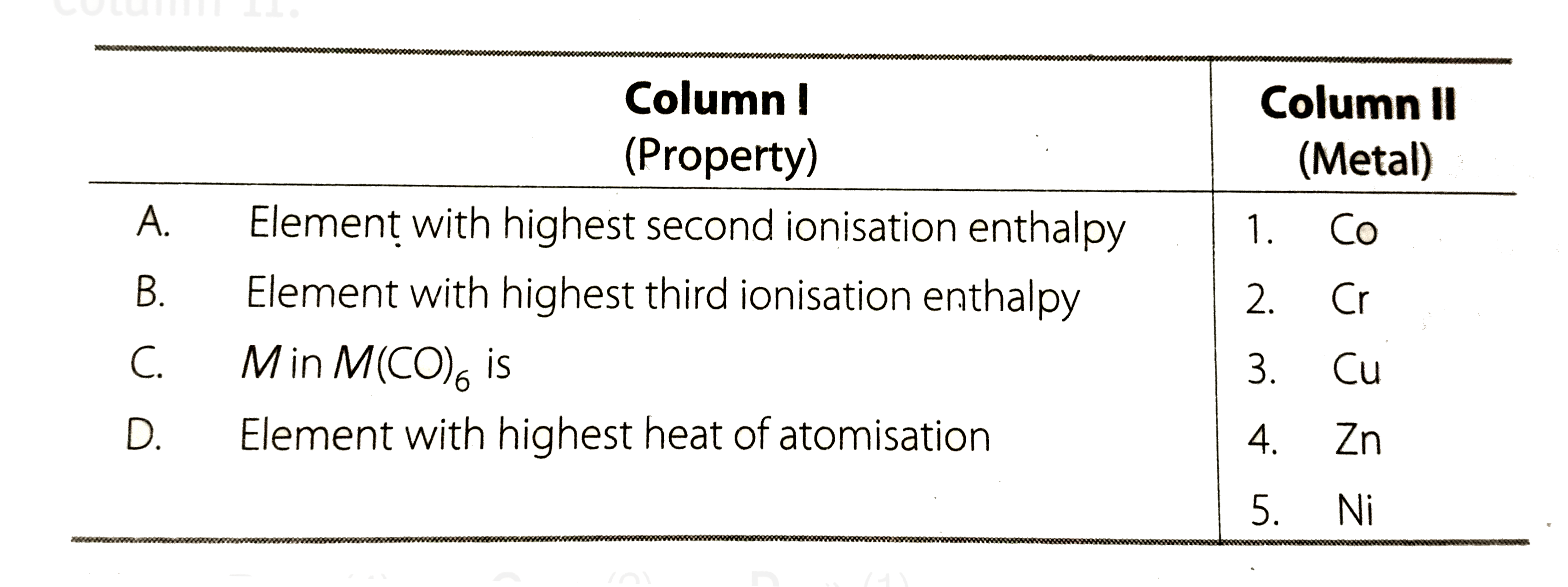 View Solution
View Solution

