Question

Find the equation of a straight line cutting off and intercept -1 from
y-axis and being equally inclined to the axes.

Explanation

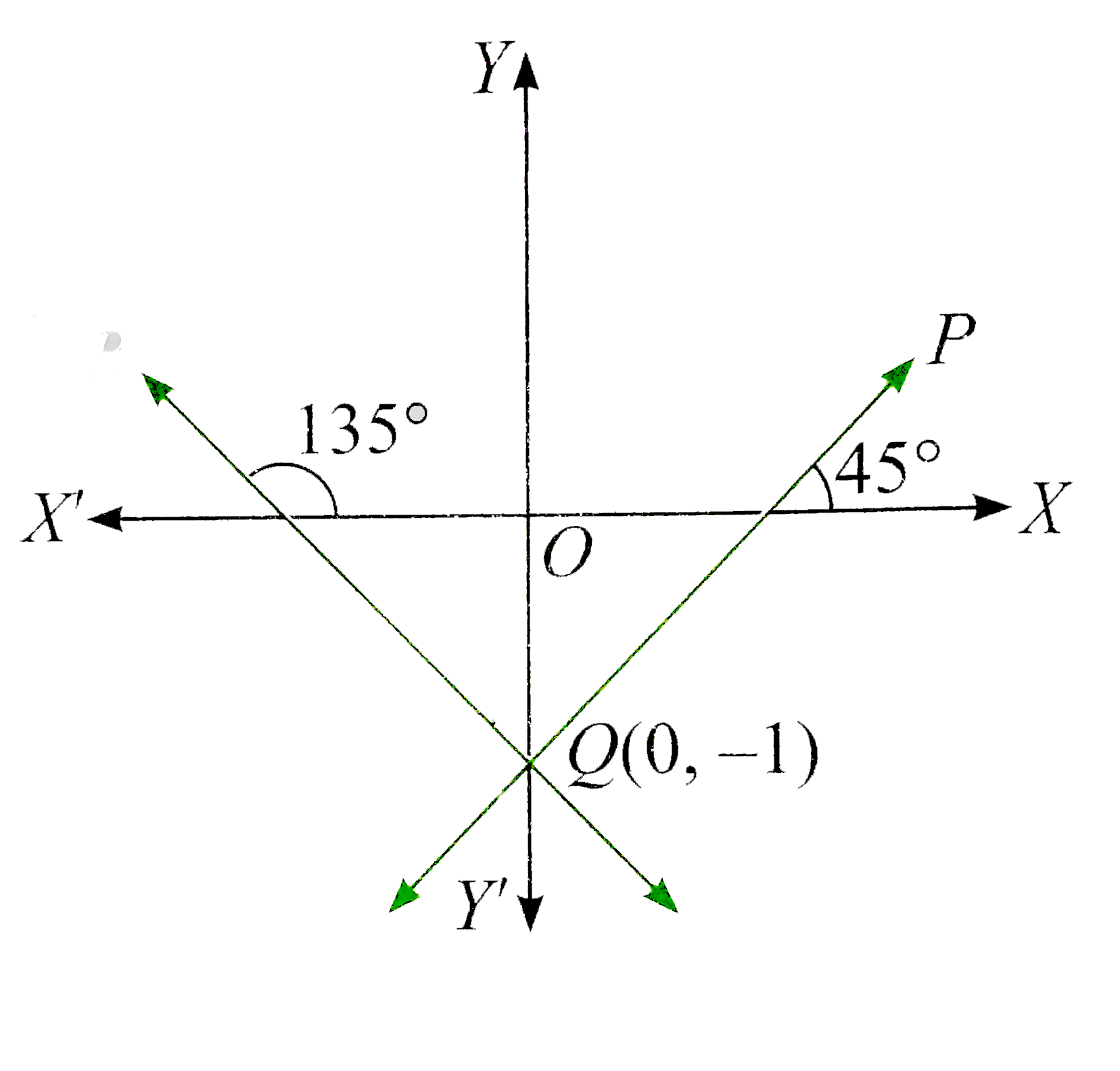
Since the required line is equally inclined with the coordinate axes, it makes an angle of either `45^(@) " or" 135^(@)` with x-axis.
So, its slope is either m = tan `45^(@) " or m" = tan 135^(@)`, i.e., m= 1 or-1.
It is given that c=-1. Hence, the equations of the lines are
y=x-1 and y=-x-1