Determine all the values of for which the point lies inside the triangle formed by the lines.
Given lines are
Draw these lines on coordinate axes.
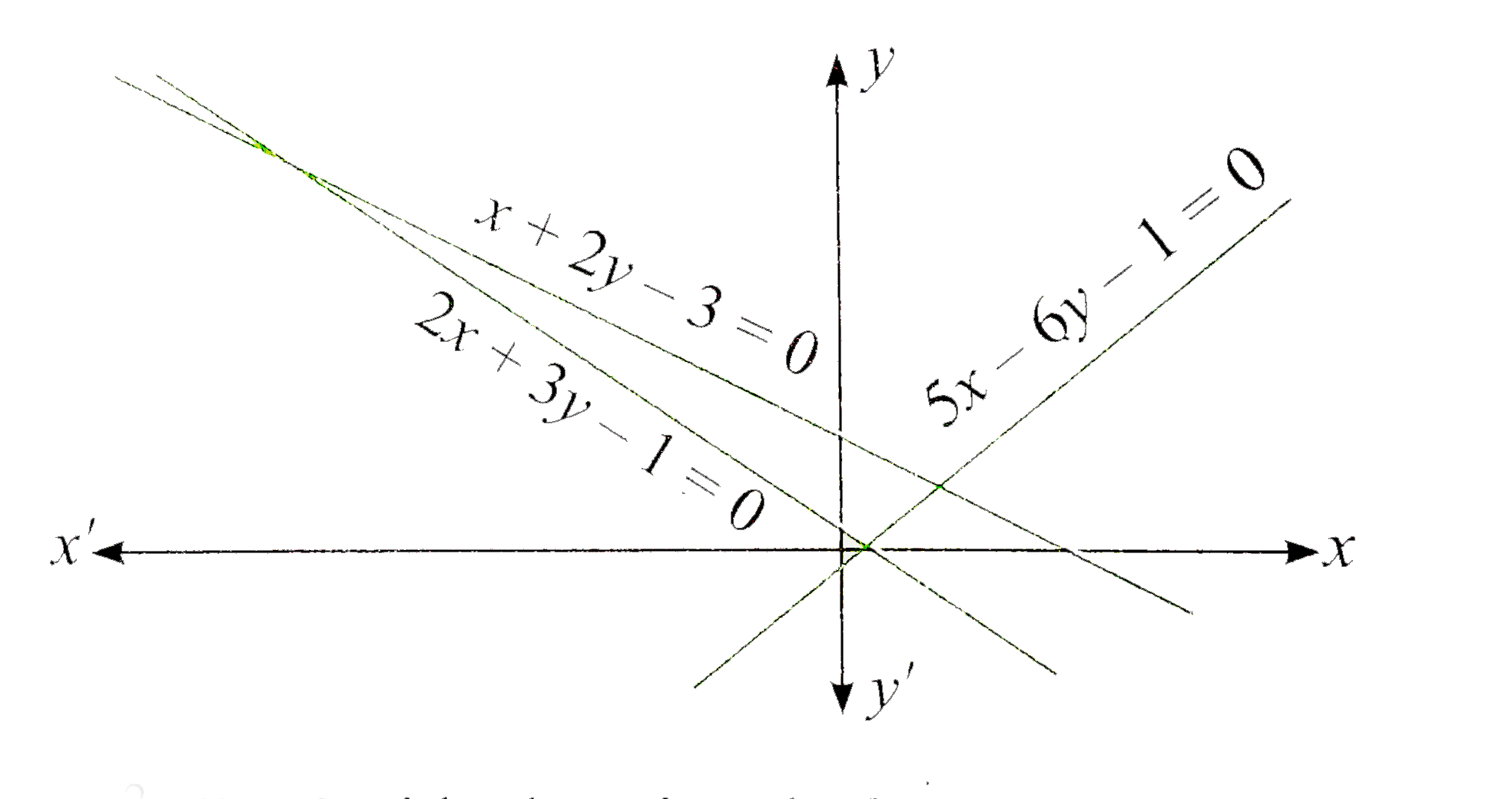
Point lies inside the triangle formed by these lines.
Clearly, from the figure, origin and point P lie on the opposite side w.r.t 2x+3y-1=0.
So, we must have
Also, origin and point P lie on the same side w.r.t line
x+2y-3=0.
So, we must have
Further origin and point P lie on the same side w.r.t. line
5x-6y-1=0.
So, we must have
From (1), (2) and (3), common values of are (-3/2,-1) (1/2,1).
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXAMPLE
12 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.1
23 Videos
- STRAIGHT LINEBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
Find the values of α so that the point P(α2,α) lies inside or on the triangle formed by the lines x−5y+6=0,x−3y+2=0andx−2y−3=0.
View SolutionFind the values of α so that the point P(α2,α) lies inside or on the triangle formed by the lines x−5y+6=0,x−3y+2=0 and x−2y−3=0.
View SolutionStatement 1: The value of α for which the point (α,α2) lies inside the triangle formed by the lines x=0,x+y=2 and 3y=x is (0,1). Statement 2: The parabola y=x2 meets the linex+y=2 at(1,1).
View SolutionFind all the values of θ for which the point (sin2θ,sinθ) lies inside the square formed by the line xy=0 and 4xy−2x−2y+1=0.
View SolutionIf point P(α,α2−2) lies inside the triangle formed by the lines x+y=1,y=x+1andy=−1 then α∈
View SolutionDetermine the range of values of 0∈[0,2π] for which (cosθ,sinθ) lies inside the triangle formed by the lines x+y−2=0,x−y−1=0and6x+2y−√10=0
View SolutionThe complete set of real values of 'a' such that the point lies triangle p(a,sina) lies inside the triangle formed by the lines x−2y+2=0;x+y=0 and x−y−π=0
View SolutionThe range of value of α such that (0,α) lies on or inside the triangle formed by the lines y + 3x + 2 = 0, 3y - 2x - 5 = 0, 4y + x - 14 =0 is
View SolutionSet of value of α for which the point (α,1) lies inside the circle x2+y2−4=0 and parabola y2=4x is
View SolutionThe complete set of values of the parameter α so that the point P(α,(1+α2)−1) does not lie outside the triangle formed by the lines L1:15y=x+1,L2:78y=118−23x and L3:y+2=0 is
View Solution
