Consider two lines $L_{1} a n d L_{2}$ given by $x - y = 0$ and $x + y = 0$ , respectively, and a moving point $P (x, y) .$ Let $d (P, L_{1}), i = 1, 2,$ represents the distance of point $P$ from the line $L_{t}$ If point $P$ moves in a certain region $R$ in such a way that $2 \leq d (P, L_{1}) + d (P, L_{2}) \leq 4$ , find the area of region $R .$

Video Solution

Text Solution

Verified by Experts

$d (P, L_{1}) = \frac{| x - y |}{\sqrt{2}}$
$and d (P, L_{2}) = \frac{| x + y |}{\sqrt{2}}$
Now, we have
$2 \leq d (P, L_{1}) + d (P, L_{2}) \leq 4$
$or 2 \sqrt{2} \leq | x - y | + | x + y | \leq 4 \sqrt{2} (1)$
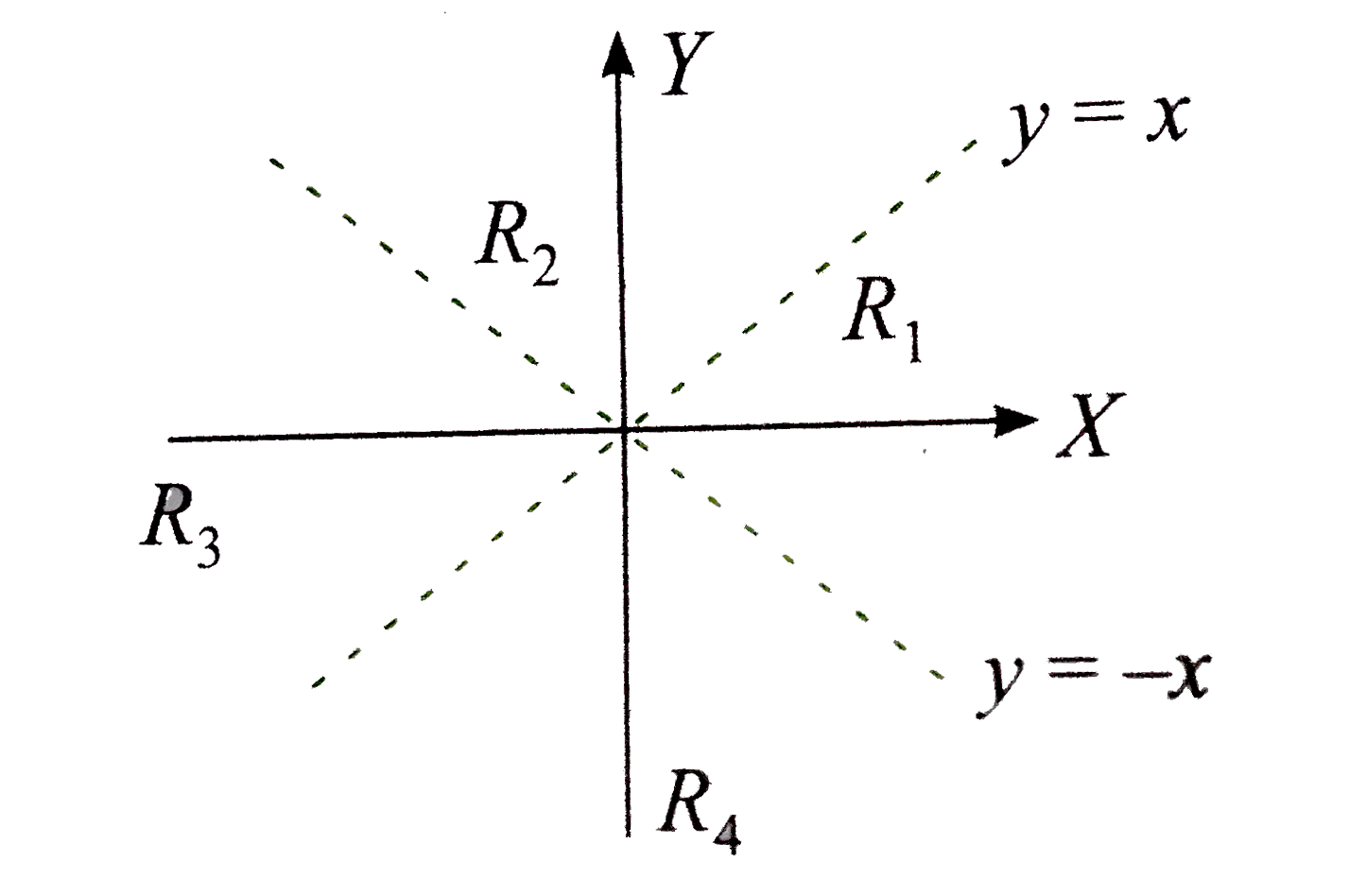
Now, let us consider the four regions, namely, $R_{1}, R_{2}, R_{3} and R_{4}, in the lines L_{1} and L_{2}$ dividing the coordinate plane.
$In R_{1}, we have y < x, y > - x . In R_{2}, we have y > x, y > - x . S i m i l a r l y,$
$In R_{3}, we have y > x, y < - x . Finally, in R_{4}, we have y < x, y < - x .$
Thus , for $R_{2},$ (1) becomes.
$2 \sqrt{2} \leq x - y + x + y \leq 4 \sqrt{2} or \sqrt{2} \leq x \leq 2 \sqrt{2}$
Similarly, for $R_{2}$ , (1) becomes
$2 \sqrt{2} \leq y - x + x + y \leq 4 \sqrt{2} or \sqrt{2} \leq y \leq 2 \sqrt{2}$
In $R_{3}$ ,(1) will become
$2 \sqrt{2} \leq y - x - x - y \leq 4 \sqrt{2} or - \sqrt{2} \leq x \leq - 2 \sqrt{2}$
Finally, in $R_{4},$ (1) will become
$2 \sqrt{2} \leq x - y - x - y \leq 4 \sqrt{2}$
$or - 2 \sqrt{2} \leq y \leq - 2 \sqrt{2}$
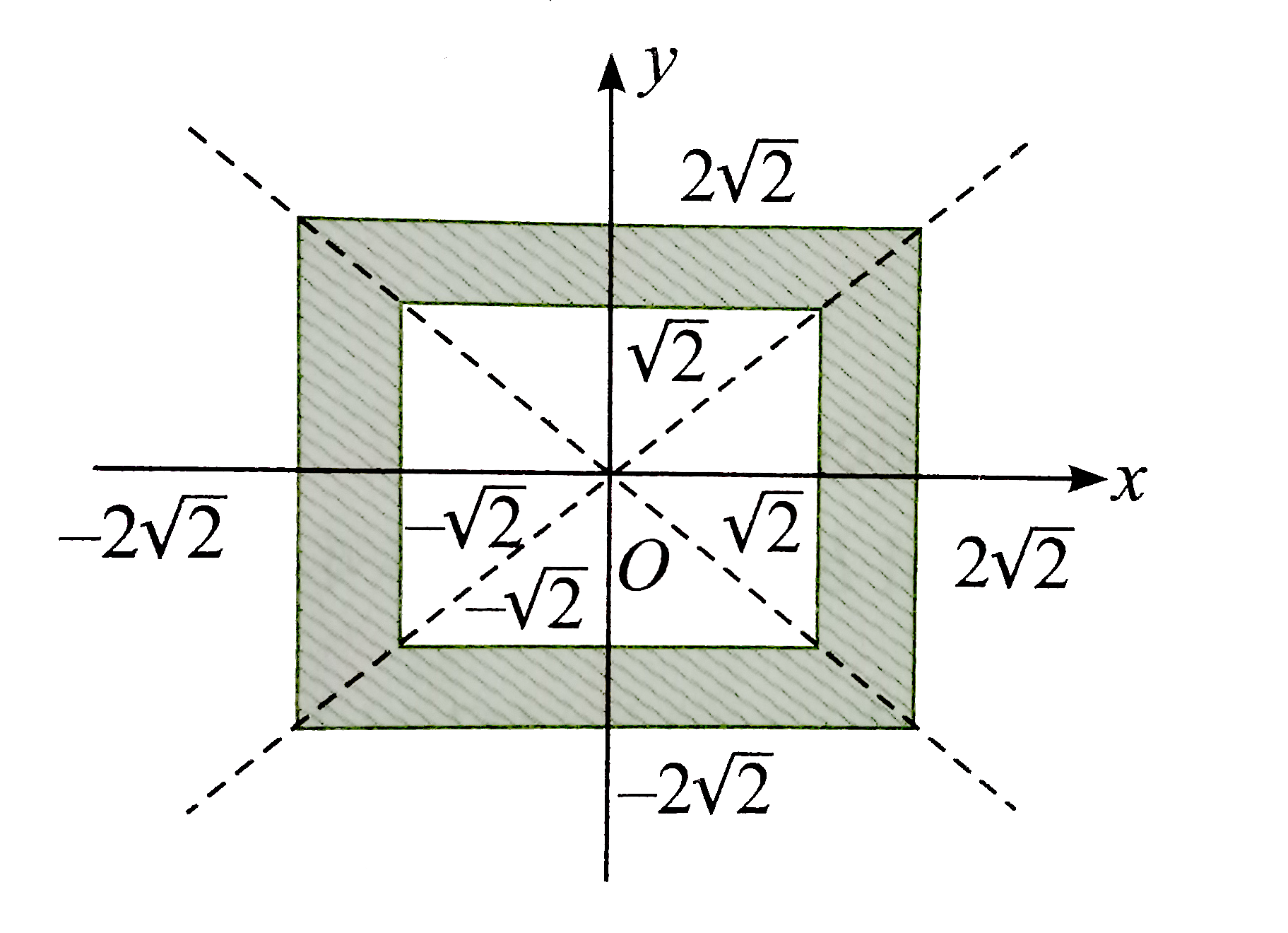
Thus region R will be the region between concentric squares formed by the lines $x = \pm \sqrt{2}, y = \pm \sqrt{2} and x = \pm 2 \sqrt{2}, y = \pm 2 \sqrt{2} .$
Thus the required are is ${(4 \sqrt{2})}^{2} - {(2 \sqrt{2})}^{2} = 24$ units.

Updated on:21/07/2023

|

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-STRAIGHT LINES-EXAMPLE

Home
Ask Doubt
Profile