If the point P(a2,a) lies in the region corresponding to the acute angle between the lines 2y=x and 4y=x , then find the values of a.
The correct Answer is:α∈(2,4)
Acute angle is formed by lines in first the third quadrants.
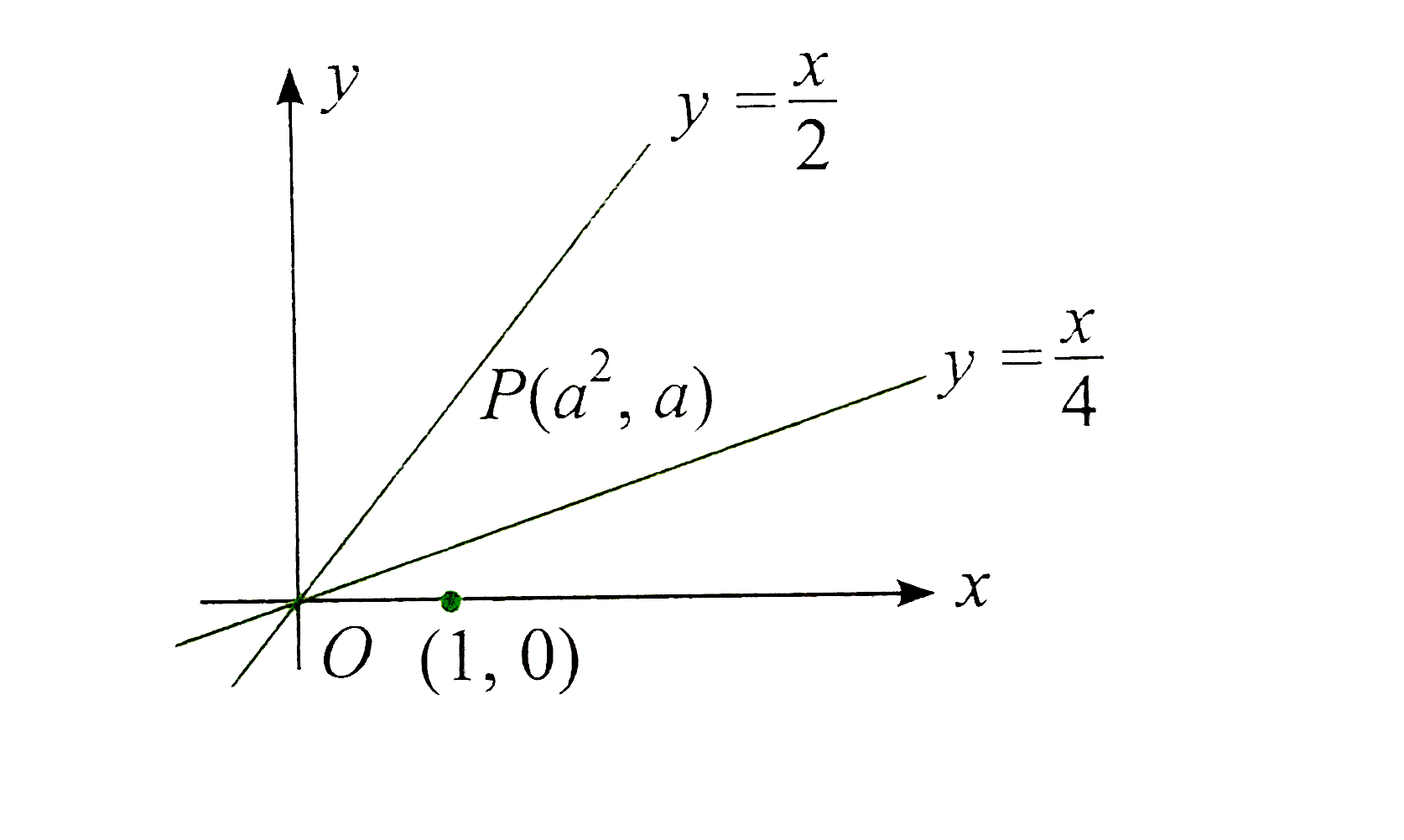
But a2>0, and hence, point P(a2,a) lies in the first quadrant.
We have a−a24>0 and a−a22<0
⇒a∈(0,4) and a∈(−∞,0)∪(2,∞)
⇒a∈(2,4)
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.58videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.65videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.37videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
If the point (1+cosθ,sinθ) lies between the region corresponding to the acute angle between the lines 3y = x and 6y = x, then
View SolutionFind the acute angle between the lines 2x−y+3=0 and x+y+2=0.
View SolutionIf the point (a,a) is placed in between the lines |x+y|=4, then find the values of a.
View SolutionIf the point (a,a) is placed in between the lines |x+y|=4, then find the values of a.
View SolutionFind the bisector of the acute angle between the lines :
3x+4y=11and12x−5y=2View SolutionFind the bisector of the acute angle between the lines :
5x=12y+24and12x=5y+10View SolutionFind the angle between the lines 2x=3y=−z and 6x=−y=−4z
View SolutionFind the angle between the lines 2x=3y=−zand6x=−y=−4z.
View SolutionFind the angle between the two lines 2x=3y=−zand6x=−y=−4z.
View SolutionUse tables to find the acute angle between the lines 2y+x=0andx1+y2=2.
View Solution

