The equation of a line through the point (1, 2) whose distance from the point (3,1) has the greatest value is (a)y=2x (b)y=x+1 (c)x+2y=5 (d) y=3x−1
y=2x
y=x+1
x+2y=5
y=3x-1
The correct Answer is:A
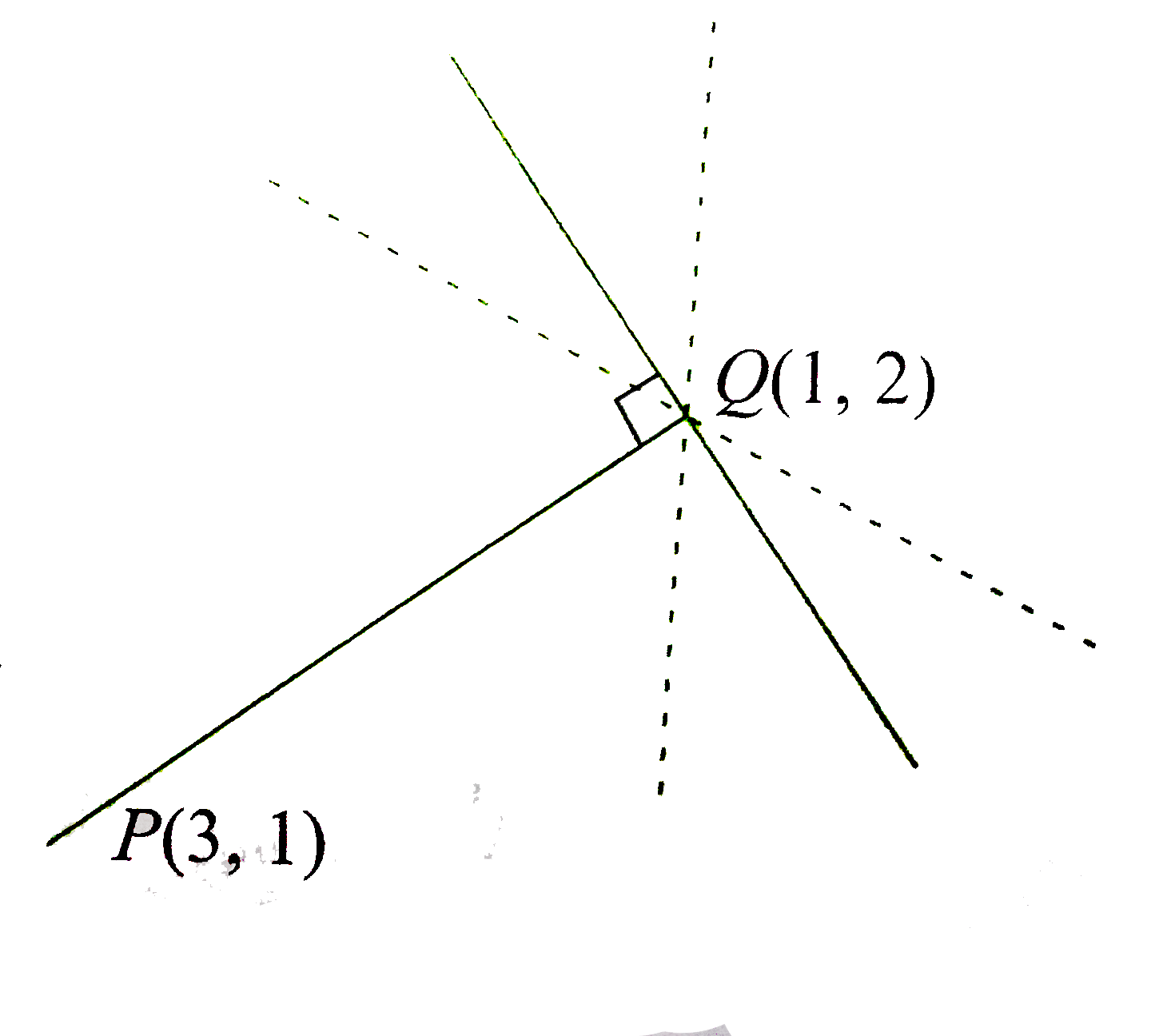
Obviously, the line through Q is at the greatest distance from point P when it is perpendicular to PQ. Now, the slope of line PQ is mPQ=−1/2. Then the slope of perpendicular line passing through Q is
y-2 = 2(x-1)
or 2x-y=0
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)30videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)27videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.65videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
Find the equation of the line through point (1,2,3) and parallel to line x−y+2z=5,3x+y+z=6.
View SolutionFind the equation of the line through point (1,2,3) and parallel to plane x−y+2z=5,3x+y+z=6
View SolutionFind the equations of the lines through the point of intersection of the lines x−y+1=0and2x−3y+5=0 whose distance from the point (3,2) is 7/5.
View SolutionThe equation of a straight line passing through the point (2, 3) and inclined at an angle of tan−1(12) with the line y+2x=5 is: (a)y=3 (b) x=2 (c)3x+4y−18=0 (d) 4x+3y−17=0
View SolutionThe equation of a straight line passing through the point (2, 3) and inclined at an angle of tan−1(12) with the line y+2x=5 y=3 (b) x=2 3x+4y−18=0 (d) 4x+3y−17=0
View SolutionFind the equations of the lines through the point of intersection of the lines x−y+1=0 and2x−3y+5=0whose distance from the point(3,2) is 75
View SolutionFind the distance of the line 2x+y=3 from the point(−1, −3) in the direction of the line whose slope is 1.
View SolutionFind the equation of a circle which passes through the point (2,0) and whose centre is the limit of the point of intersection of the lines 3x+5y=1and(2+c)x+5c2y=1 as c tends to 1.
View Solutiondistance of the lines 2x−3y−4=0 from the point (1,1) measured paralel to the line x+y=1 is
View SolutionFind the equation of a circle which passes through the point (2,0) and whose centre is the point of intersection of the lines 3x+5y=1, (2+c)x+5c2y=1 where limit of c tends to 1.
View Solution

