In an isoceles triangle OAB , O is the origin and OA=OB=6 . The equation of the side AB is x-y+1=0 Then the area of the triangle is
2√21
√142
√1422
√712
The correct Answer is:D
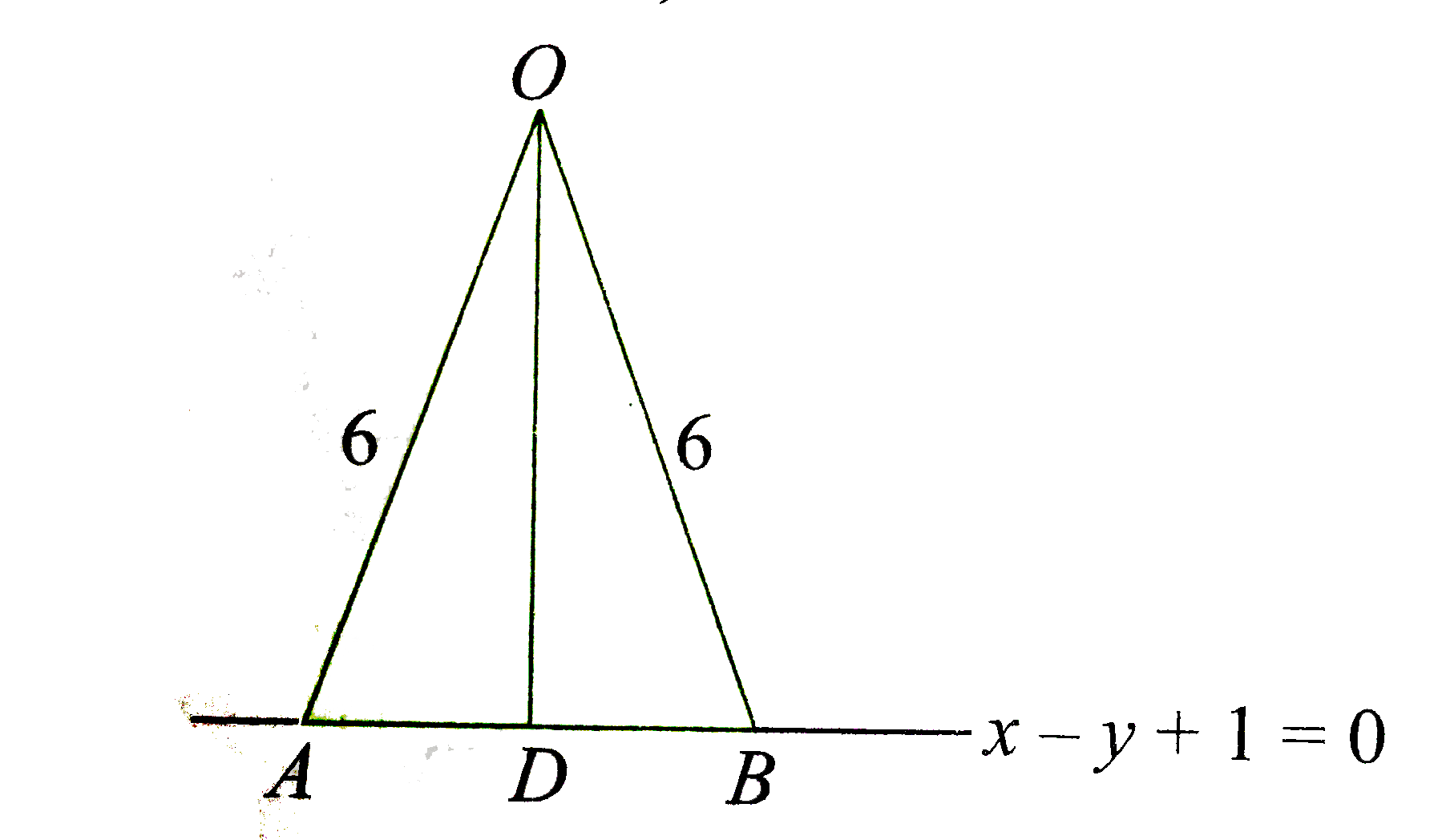
Let D be the midpoint of AB.
OD=1√2
AD=√62−OD2=√36−12=√172
∴Area of triangle=12×AB×OD=√172×√12=√712
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)30videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)27videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.65videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
If the ends of the base of an isosceles triangle are at (2, 0) and (0, 1), and the equation of one side is x=2, then the orthocenter of the triangle is
View SolutionIf a vertex of an equilateral triangle is the origin and the side opposite to it has the equation x+y=1, then orthocentre of the triangle is :
View SolutionLet ΔABC is an isosceles trianlge with AB=AC. If B=(0,a),C=(2a,0) and the equation of AB is 3x−4y+4a=0, then the equation of side AC is
View SolutionIn triangle ABC , the equation of side BC is x−y=0. The circumcenter and orthocentre of triangle are (2, 3) and (5, 8), respectively. The equation of the circumcirle of the triangle is a) x2+y2−4x+6y−27=0 b) x2+y2−4x−6y−27=0 c) x2+y2+4x−6y−27=0 d) x2+y2+4x+6y−27=0
View SolutionThe equation of the sides of a triangle are x+2y+1=0,2x+y+2=0andpx+qy+1=0 and area of triangle is Δ .
View SolutionIf a plane cuts off intercepts OA=a,OB=b,OC=c from the coordinate axes 9where 'O' is the origin). then the area of the triangle ABC is equal to
View SolutionLet O be an interior point of triangle ABC, such that 2−−→OA+3−−→OB+4−−→OC=0, then the ratio of the area of ΔABC to the area of ΔAOC is
View SolutionIf the point 3x+4y−24=0 intersects the X-axis at the point A and the Y-axis at the point B, then the incentre of the triangle OAB, where O is the origin, is
View SolutionLet A(2,0) and B(z) are two points on the circle |z|=2. M(z') is the point on AB. If the point ¯z' lies on the median of the triangle OAB where O is origin, then arg(z') is
View SolutionThe co-ordinates of the vertex of an equilateral triangle are (2,−1) and equation of its base is x+y−1=0. Find the equations of its other two sides.
View Solution

