The point (2,1) , translated parallel to the line x−y=3 by the distance of 4 units. If this new position A' is in the third quadrant, then the coordinates of A' are-
(2+2√2,1+2√2)
(−2+√2,−1−2√2)
(2−2√2,1−2√2)
none of these
The correct Answer is:C
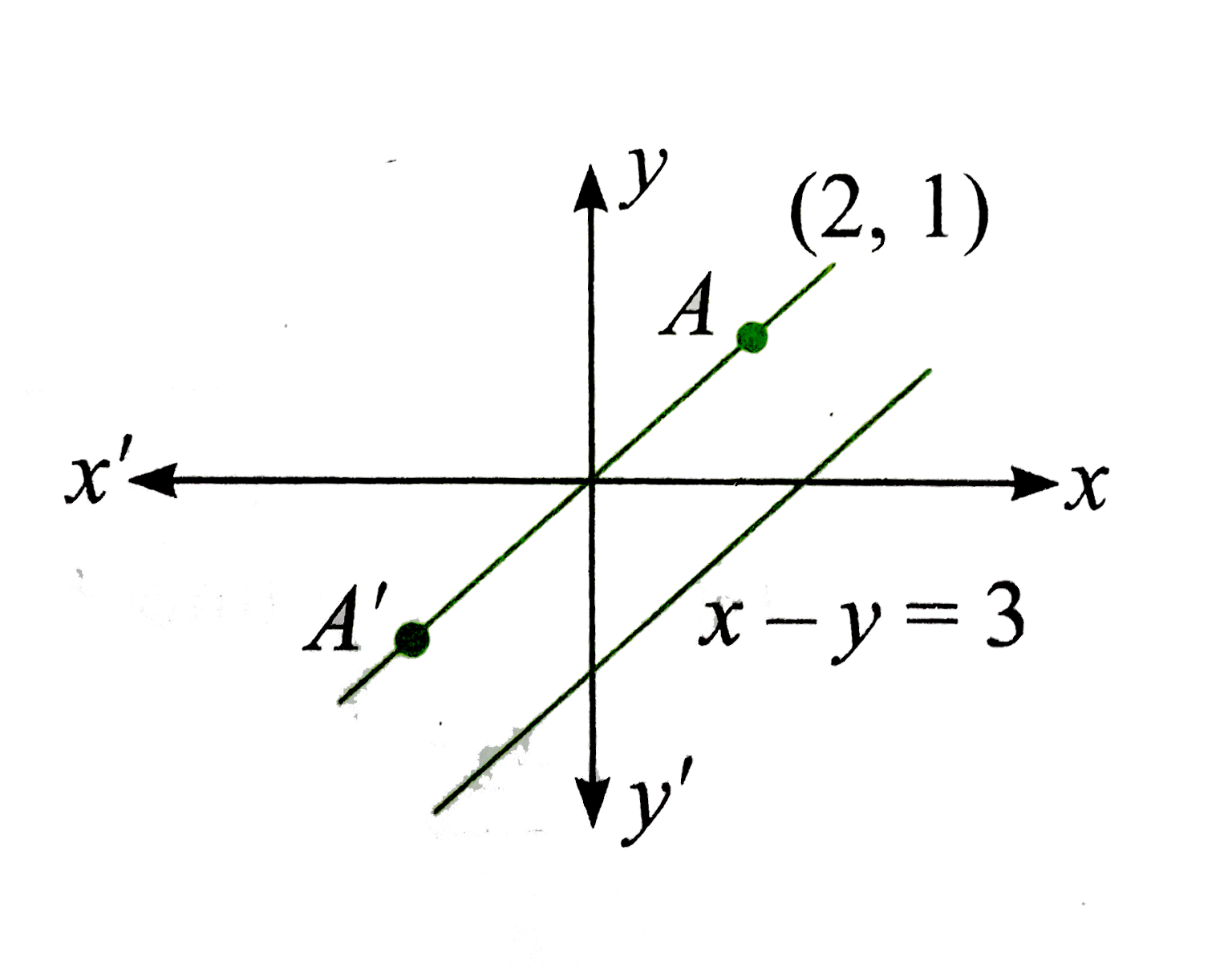
Since the poinnt A(2,1) is translated parallel to x-y=3, A'A has the same slope as that of x-y=3. Therefore, A'A passes through (2,1) and has slope 1. Here, tanθ=1or cosθ=1√2,sinθ=1√2.
Thus, the equation of AA' is
x−2cos(π/4)=y−1sin(π/4)
Since AA' =4, the coordinates of A' are given by
x−2cos(π/4)=y−1sin(π/4)=−4
or x=2−4cosπ4,y=1−4sinπ4
or x=2−2√2,y=1−2√2
Hence, the coordinates of A' are (2−2√2,1−2√2).
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)
30 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)
27 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
The point A(2,1) is translated parallel to the line x−y=3 by a distance of 4 units. If the new position A' is in the third quadrant, then the coordinates of A' are (A) (2+2√2,1+2√2 (B) (−2+√2,−1−2√2) (C) (2−2√2 , 1−2√2) (D) none of these
View SolutionThe point (2,1) is translated parallel to the line L:x−y=4 by 2√3units. If the new point Q lies in the third quadrant, then the equation of the line passing through Q and perpendicular to L is
View SolutionThe point (2,1) is translated parallel to the line L:x−y=4 by 2√3units. If the new point Q lies in the third quadrant, then the equation of the line passing through Q and perpendicular to L is
View SolutionThe point P(1,1) is transiated parallel to 2x=yin the first quadrant through a unith distance. The coordinates of the point in new position are
View SolutionThe point (1,−2) is reflected in the x-axis and then translated parallel to the positive direction of x-axis through a distance of 3 units, find the coordinates of the point in the new position.
View SolutionA line is drawn through the point A(4,−1) and parallel to the line 3x−4y+7=0. Find the coordinates of two points on this line which are at distance of 5 units from A.
View SolutionThe point P(1,1) is translated parallel to 2x=y in the first quadrant through a unit distance. The coordinates of the point P in the new position are (1±2√5,1±1√5) (1±1√5,1±2√5) (1√5,2√5) (4) (2√5,1√5)
View SolutionThe point A(2,1) is shifted by 3√2 unit distance parallel to the line x+y=1 in the direction of increasing ordinate to reach a point B. Find the image of B by the line x+y=1.
View Solutiona line drawn through A(4,−1) parallel to the line 3x−4y+1=0. Find the coordinates of two points on this line which are at a distance of 5 units from A
View SolutionFind the equations of lines parallel to 3x−4y−5=0 at a unit distance from it.
View Solution
