Question

Consider point P(x, y) in first quadrant. Its reflection about x-axis is ${\displaystyle Q(x_1,y_1)}$. So, ${\displaystyle x_1=x}$ and ${\displaystyle y\left(1\right)=-y}$.
This may be written as : ${\displaystyle \{\begin{array}{l}{x}_1=1.x+0.y\\ y_1=0.x+(-1)y\end{array}}$
This system of equations can be put in the matrix as :
${\displaystyle \left[\begin{array}{c}{x}_1\\ y_1\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]}$
Here, matrix ${\displaystyle \left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]}$ is the matrix of reflection about x-axis. Then find the matrix of reflection about the line ${\displaystyle y=x}$.

Explanation

(i) Reflection of (x, y) about y-axis is `(x_(1), y_(1)) equiv (-x, y)`.
`:. x_(1)=(-1)x+0y`
and `y_(1)=0x+y`
`:. [(x_(1)),(y_(1))]=[(-1,0),(0,1)][(x),(y)]`
(ii) Reflection of (x, y) about the line `y=x` is `(x_(1), y_(1)) equiv (y, x)`.
`:. x_(1)=0x+y`
`y_(1)=x+0y`
`:. [(x_(1)),(y_(1))]=[(0,1),(1,0)][(x),(y)]`
(iii) Reflection of (x, y) about origin is `(x_(1), y_(1)) equiv (-x, -y)`.
`:. x_(1)=-x+0y`
`y_(1)=0x-y`
`:. [(x_(1)),(y_(1))]=[(-1,0),(0,-1)][(x),(y)]`
(iv) Reflecton in line `t=x tan theta` or `(sin theta)x-(cos theta)y=0`:

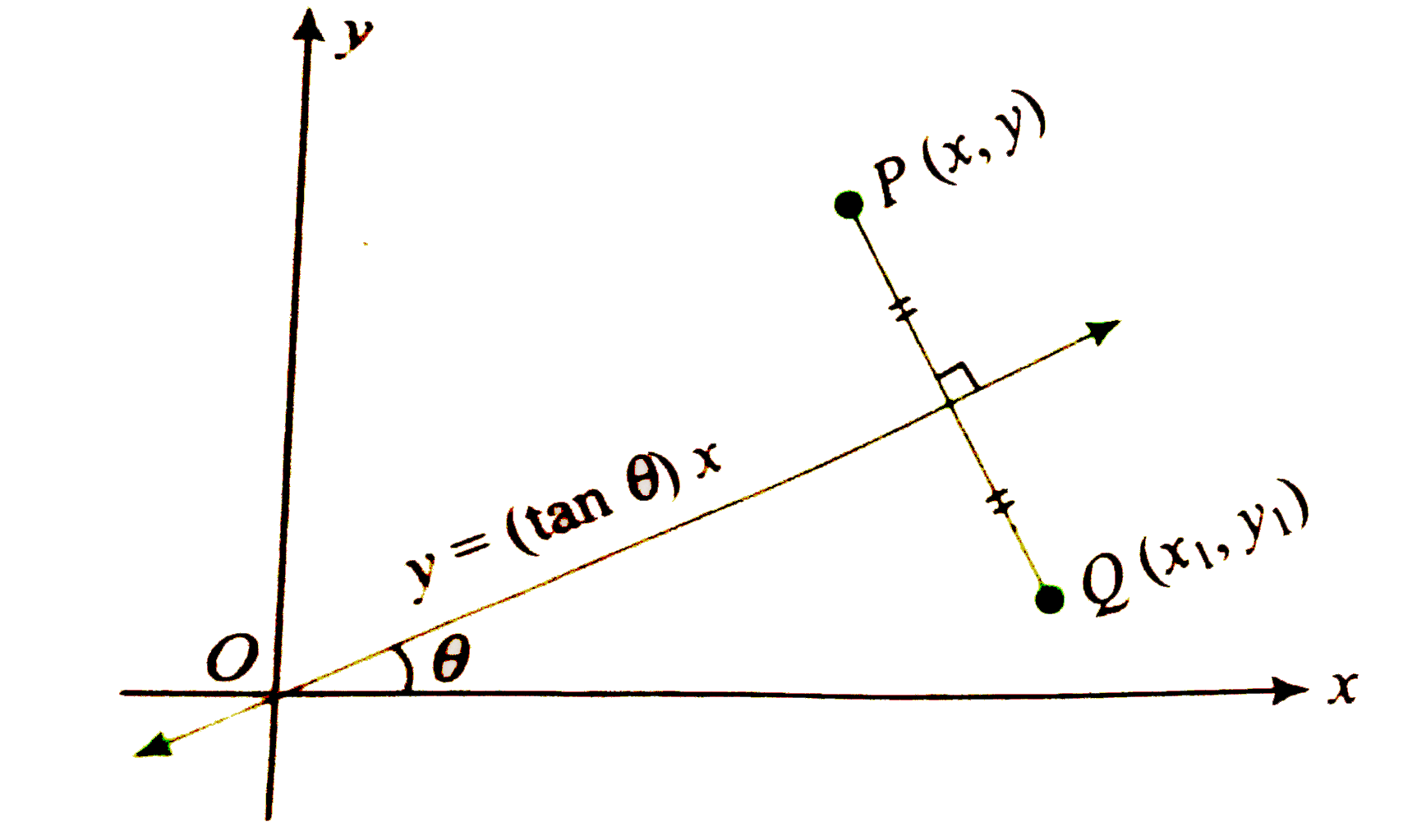
We kanow that
`(x_(1)-x)/(sin theta)=(y_(1)-y)/(- cos theta)=(-2((sin theta)x-(cos theta)y))/(sin^(2) theta+cos^(2) theta)`
`:. x_(1)=(1-2 sin^(2) theta)x+(2 sin theta cos theta)y`
or `x_(1)=(cos 2 theta)x+(sin 2 theta) y`
`y_(1)=(2 sin theta cos theta)x+ (1-2 cos^(2) theta)y`
or `y_(1)=(sin 2 theta)x-(cos 2 theta)y`
Thus, `[(x_(1)),(y_(1))]=[(cos 2 theta,sin 2 theta),(sin 2 theta,- cos 2 theta)][(x),(y)]`
By putting `theta=0, pi//2, pi//4`, we can get the reflection matrices x-axis, y-axis and the line y=x, respectively.