Show that the characteristics roots of an idempotent matris are either 0 or 1
To show that the characteristic roots (eigenvalues) of an idempotent matrix are either 0 or 1, we will follow these steps:
Step 1: Definition of Idempotent Matrix
An idempotent matrix A is defined as a matrix that satisfies the equation:
A2=A
Step 2: Eigenvalue Equation
Let λ be an eigenvalue of the matrix A and x be the corresponding eigenvector. By definition of eigenvalues, we have:
Ax=λx
Step 3: Applying the Idempotent Property
Now, applying the idempotent property A2=A to the eigenvalue equation:
A2x=Ax
Substituting Ax=λx into the left-hand side gives:
A(λx)=λAx
This simplifies to:
A(λx)=λ2x
Step 4: Equating the Two Expressions
From the idempotent property, we also have:
Ax=λx
Thus, we can write:
λ2x=λx
Step 5: Rearranging the Equation
Rearranging the equation gives:
λ2x−λx=0
Factoring out x (which is not zero) gives:
x(λ2−λ)=0
Step 6: Solving the Factorized Equation
Since x≠0, we can set the factor equal to zero:
λ2−λ=0
Factoring this gives:
λ(λ−1)=0
Step 7: Finding the Eigenvalues
From this equation, we find the solutions:
λ=0orλ=1
Conclusion
Thus, we have shown that the characteristic roots (eigenvalues) of an idempotent matrix are either 0 or 1.
---
An idempotent matrix A is defined as a matrix that satisfies the equation:
A2=A
Let λ be an eigenvalue of the matrix A and x be the corresponding eigenvector. By definition of eigenvalues, we have:
Ax=λx
Now, applying the idempotent property A2=A to the eigenvalue equation:
A2x=Ax
Substituting Ax=λx into the left-hand side gives:
A(λx)=λAx
This simplifies to:
A(λx)=λ2x
From the idempotent property, we also have:
Ax=λx
Thus, we can write:
λ2x=λx
Rearranging the equation gives:
λ2x−λx=0
Factoring out x (which is not zero) gives:
x(λ2−λ)=0
Since x≠0, we can set the factor equal to zero:
λ2−λ=0
Factoring this gives:
λ(λ−1)=0
From this equation, we find the solutions:
λ=0orλ=1
Thus, we have shown that the characteristic roots (eigenvalues) of an idempotent matrix are either 0 or 1.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - Exercises65videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - Multiple Correct Answer49videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - CAE 13.412videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATHMETICAL REASONINGEXERCISE - Archives10videos
MATHMETICAL REASONING
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
Similar Questions
Coralloid roots are the characteristics of :
View SolutionNodulated roots are characteristic of family
View SolutionIf q is a characteristic root of an singular matrix A, then prove that |A|q is a characteristic root of a adj A.
View SolutionIf α is a characteristic root of a nonsin-gular matrix, then prove that |A|α is a characteristic root of adj A.
View SolutionState three characteristics that show a chemical reaction has occurred.
View SolutionWhat are the structural characteristics of
(a) meristematic cells near root tip
(b) the cells in the eleongation zone of the rootView SolutionList the characteristics of root hair that make it suitable for absorbing water.
View SolutionSome characteristics of velocity on displacement-time graph are show on graphs below. Which graph correctly represents the characteristics :

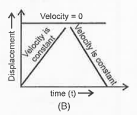
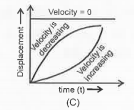
 View Solution
View SolutionA major characteristic of the monocot root is the presence of
View SolutionA major characteristic of the monocot root is the presence of
View Solution

