If A=[ab0a] is nth root of I2, then choose the correct statements: If n is odd, a=1,b=0 If n is odd, a=−1,b=0 If n is even, a=1,b=0 If n is even, a=−1,b=0 a. i, ii, iii, iv b. ii, iii, iv c. i, ii, iii, iv d. i, iii, iv
i, ii, iii
ii, iii, iv
i, ii, iii, iv
i, iii, iv
The correct Answer is:D
To solve the problem, we need to determine the conditions under which the matrix A=(ab0a) is an n-th root of the identity matrix I2. This means that An=I2.
1. Define the Matrix A:
A=(ab0a)
2. Calculate A2:
A2=A⋅A=(ab0a)⋅(ab0a)=(a2ab+ba0a2)=(a22ab0a2)
3. Calculate A3:
A3=A2⋅A=(a22ab0a2)⋅(ab0a)=(a3a2b+2ab0a3)=(a33a2b0a3)
4. General Form of An:
By observing the pattern, we can generalize:
An=(annan−1b0an)
5. Set An=I2:
We need An=I2=(1001). This gives us two equations:
an=1andnan−1b=0
6. Analyze the equations:
- From an=1, we have:
- a=1 or a=−1 (since an=1 for any integer n).
- From nan−1b=0:
- If n≠0, then b=0 (since an−1 cannot be zero if a is either 1 or -1).
7. Determine conditions based on n:
- If n is odd:
- a=1 and b=0 is valid.
- a=−1 and b=0 is also valid.
- If n is even:
- a=1 and b=0 is valid.
- a=−1 and b=0 is also valid.
Conclusion:
Thus, we can conclude:
- If n is odd, both a=1,b=0 and a=−1,b=0 are valid.
- If n is even, both a=1,b=0 and a=−1,b=0 are valid.
Correct Statements:
- If n is odd, a=1,b=0 (True).
- If n is odd, a=−1,b=0 (True).
- If n is even, a=1,b=0 (True).
- If n is even, a=−1,b=0 (True).
Thus, the correct answer is option d: i, iii, iv.
A=(ab0a)
A2=A⋅A=(ab0a)⋅(ab0a)=(a2ab+ba0a2)=(a22ab0a2)
A3=A2⋅A=(a22ab0a2)⋅(ab0a)=(a3a2b+2ab0a3)=(a33a2b0a3)
By observing the pattern, we can generalize:
An=(annan−1b0an)
We need An=I2=(1001). This gives us two equations:
an=1andnan−1b=0
- From an=1, we have:
- a=1 or a=−1 (since an=1 for any integer n).
- From nan−1b=0:
- If n≠0, then b=0 (since an−1 cannot be zero if a is either 1 or -1).
- If n is odd:
- a=1 and b=0 is valid.
- a=−1 and b=0 is also valid.
- If n is even:
- a=1 and b=0 is valid.
- a=−1 and b=0 is also valid.
Thus, we can conclude:
- If n is odd, both a=1,b=0 and a=−1,b=0 are valid.
- If n is even, both a=1,b=0 and a=−1,b=0 are valid.
- If n is odd, a=1,b=0 (True).
- If n is odd, a=−1,b=0 (True).
- If n is even, a=1,b=0 (True).
- If n is even, a=−1,b=0 (True).
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - Multiple Correct Answer49videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - Linked Comprehension Type27videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - CAE 13.517videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATHMETICAL REASONINGEXERCISE - Archives10videos
MATHMETICAL REASONING
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
Similar Questions
Knowledge Check
- Question 1 - Select One
If n is an odd natural number, then n(n2−1) is divisible by:
(i) 24
(ii) 48
(iii) 120
(iv) 64A24B48C120D64
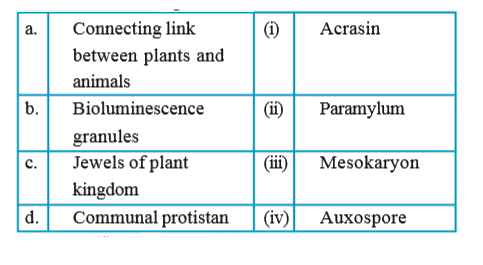
Find the correct matches

(1) a-iii, b-i, c-iv, d-ii
(2) a-ii, b-i, c-iii, d-iv
(3) a-iii, b-iv, c-ii, d-i
(4) a-iv, b-iii, c-I, d-iiView SolutionMatch the following and mark the correct option :

a -v , b- iv , c - ii , d - iii , e - i
a -ii , b- iv , c - v , d - iii , e - i
a -ii , b- i , c - v , d - iv , e - iii
a -v , b- iii , c - ii , d - iv , e - iView SolutionMatch the animals given in column A with their location in column B.
Column AColumn B(i)DodoA.Africa(ii)QuaggaB.Russia(iii)ThylacineC.Mauritius(iv)Stellar's sea cowD.Australia
Choose the correct match from the following.
(a) i-A, ii-C, iii-B, iv-D
(b) i-D, ii-C, iii-A, iv-B
(c) i-C, ii-A, iii-B, iv-D
(d) i-C, ii-A, iii-D, iv-BView SolutionMatch the following and choose the correct option
(i) Physalia a. Sea anemone(ii) Meandrina b. Brain coral(iii) Gorgonia c. Sea fan(iv) Adamsia d. Portuguese man of war
(1) i-d, ii-b, iii-c, iv-a
(2) i-c, ii-b, iii-b, iv-a
(3) i-d, ii-c, iii-a, iv-a
(4) i-b, ii-c, iii-a, iv-dView SolutionAccording to IUCN, some of the extinctions include
(i) Dodo
(ii) Indian gazelle
(iii) Thylacine
(iv) Steller's sea cow
(a) (i), (ii), (iii) and (iv)
(b) (ii) and (iv)
(c) (i),(iii) and (iv)
(d) (iii) and (iv)View SolutionUse the given Venn-diagram to find:
(i) B-A
(ii) A
(iii) B'
(iv) A∩B
(v) A∪B
 View Solution
View SolutionMatch Column - I with Column - II and select the CORRECT option form the codes given below
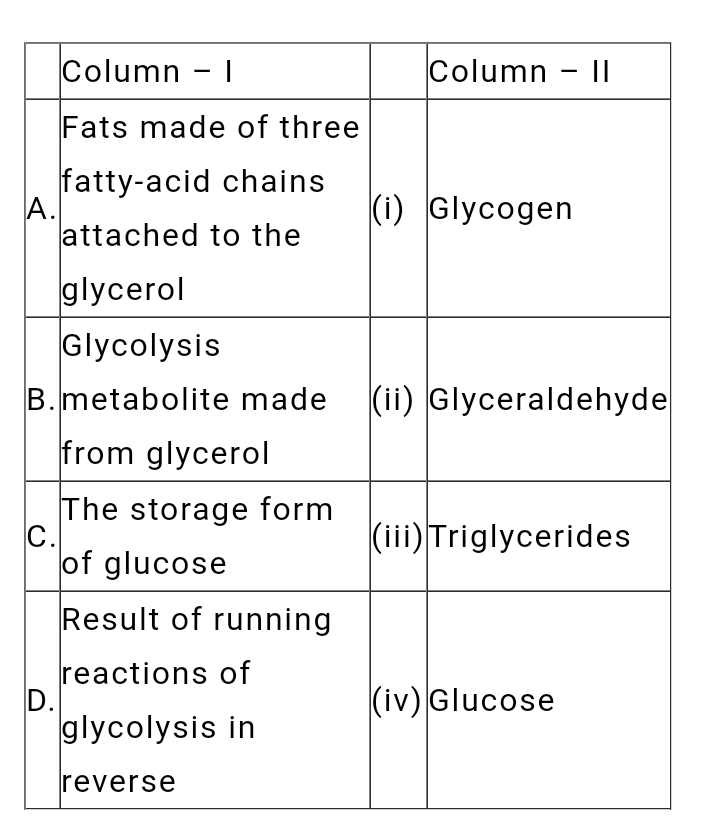
(a) A - (iv) , B - (ii) , C - (i) , D - (iii)
(b) A - (iii) , B - (ii) , C - (i) , D - (iv)
(c) A - (iv) , B - (iii) , C - (i) , D - (ii)
(d) A - (i) , B - (ii) , C - (iii) , D - (iv)View Solution